解析延拓

解析延拓（有时简称为“延拓”）提供了一种扩展定义域的方法，在该定义域上定义了复函数。最常见的应用是对于在点 附近由幂级数确定的复解析函数

(1)

这样的幂级数展开通常仅在其收敛半径内有效。但是，在有利的情况下（幸运的是这种情况也很常见！），函数 将具有一个幂级数展开，该展开在大于预期的收敛半径内有效，并且此幂级数可用于在其原始定义域之外定义函数。例如，这允许将三角函数、指数函数、对数函数、幂函数和双曲函数的定义从实线 自然地扩展到整个复平面 。类似地，解析延拓可以用于跨越复平面中的支割线扩展解析函数的值。

设 和 分别是在域 和 上的解析函数，并假设交集 非空，并且在 上 。那么 称为 到 的解析延拓，反之亦然（Flanigan 1983，第 234 页）。此外，如果存在，则 到 的解析延拓是唯一的。

解析延拓的这种唯一性是一个相当惊人和极其有力的陈述。它实际上表明，知道复函数在某个有限复域中的值，就可以唯一地确定该函数在每个其他点的值。

通过解析延拓，从函数的任何一个幂级数表示开始，可以找到任意数量的其他幂级数，这些幂级数共同定义了函数在域的所有点的值。此外，可以从一个点到达任何点，而无需通过函数的奇点，并且由此获得的所有幂级数的集合构成了函数的解析表达式（Whittaker 和 Watson 1990，第 97 页）。

解析延拓可能导致一些有趣的现象，例如多值函数。例如，考虑平方根函数 的解析延拓。尽管此函数不是全局良好定义的（因为每个非零数都有两个平方根），但 在 附近具有良好定义的泰勒级数，

			(2)
			(3)

这可以用来扩展定义 的域。请注意，当 时， 的幂级数的收敛半径为 1。

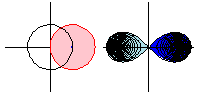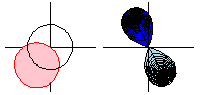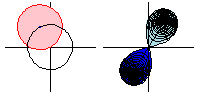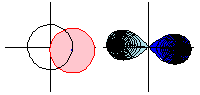
上面的动画显示了函数 沿路径 的解析延拓。请注意，当函数绕一圈时， 是原始函数的负数，因此绕两圈会将函数返回到其原始值。

在动画中，定义域空间（粉色；左图）通过平方根函数映射到像空间（蓝色；右图），浅蓝色区域表示负平方根。但是，通过围绕圆继续函数，平方根函数取值在曾经是浅蓝色区域的区域中，因此蓝色和浅蓝色区域的角色颠倒了。

这可以解释为从多值平方根函数的一个分支到另一个分支。这说明解析延拓使用附近的提供幂级数信息的值来扩展函数。

函数有可能永远不会返回到相同的值。例如， 每次绕零点延拓时都会增加 。自然域是一个函数可以解析延拓为单值函数的最大域链。对于 ，它是穿孔平面的连通无限覆盖，对于 ，它是连通双覆盖。如果存在函数无法扩展的边界，则称为自然边界。例如，在单位圆盘中存在一个亚纯函数 ，其中单位圆上的每个点都是极点集的极限点。那么圆是 的自然边界。