主题
Search

双曲余切

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook
Coth
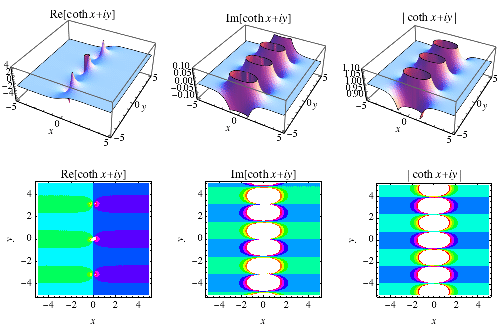
CothReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

双曲余切的定义为

cothz=(e^z+e^(-z))/(e^z-e^(-z))=(e^(2z)+1)/(e^(2z)-1).
(1)

有时也使用符号 cthz (Gradshteyn and Ryzhik 2000, p. xxix)。它在 Wolfram 语言中被实现为Coth[z].

双曲余切满足恒等式

coth(z/2)-cothz=cschz,
(2)

其中 cschz 是双曲余割。

它有一个唯一的实数不动点，其中

cothu=u
(3)

在 u^*=1.19967874... (OEIS A085984)，它与解开普勒方程中的拉普拉斯极限有关。

导数由下式给出

d/(dz)cothz=-csch^2z,
(4)

其中 cschz 是双曲余割，不定积分由下式给出

intcothzdz=ln(sinhz)+C,
(5)

其中 C 是积分常数。

洛朗级数 cothz 由下式给出

cothz=1/z+sum_(n=1)^(infty)(2^(2n)B_(2n))/((2n)!)z^(2n-1)
(6)
=1/z+1/3z-1/(45)z^3+2/(945)z^5-...
(7)

(OEIS A002431 和 A036278)，其中 B_n 是伯努利数，而 B_n(z) 是伯努利多项式。关于实数线上无穷远的渐近级数由下式给出

cothz∼1+2e^(-2z)+2e^(-4z)+....
(8)

另请参阅

伯努利数, 双极坐标, 双极柱坐标, 余切, 双曲函数, 双曲正切, 反双曲余切, 拉普拉斯方程--环面坐标, 勒贝格常数, 长球面坐标, 旋转曲面, 环面坐标, 环面函数

使用 Wolfram|Alpha 探索

参考文献

Abramowitz, M. 和 Stegun, I. A. (编). "双曲函数." §4.5 在 数学函数手册，包含公式、图表和数学表格，第 9 次印刷。 New York: Dover, 页码 83-86, 1972.Gradshteyn, I. S. 和 Ryzhik, I. M. 积分表、级数表和乘积表，第 6 版。 San Diego, CA: Academic Press, 2000.Jeffrey, A. "双曲恒等式." §2.5 在 数学公式和积分手册，第 2 版。 Orlando, FL: Academic Press, 页码 117-122, 2000.Sloane, N. J. A. 序列 A002431/M0124 和 A036278 在 "整数序列在线百科全书" 中。Spanier, J. 和 Oldham, K. B. "双曲正切 tanh(x) 和余切 coth(x) 函数." 第 30 章 在 函数图集。 Washington, DC: Hemisphere, 页码 279-284, 1987.Zwillinger, D. (编). "双曲函数." §6.7 在 CRC 标准数学表格和公式手册。 Boca Raton, FL: CRC Press, 页码 476-481 1995.Sloane, N. J. A. 序列 A010050 和 A085984 在 "整数序列在线百科全书" 中。

在 Wolfram|Alpha 中被引用

双曲余切

请引用为

Weisstein, Eric W. "双曲余切。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/HyperbolicCotangent.html

主题分类