完整群

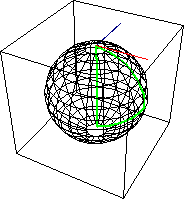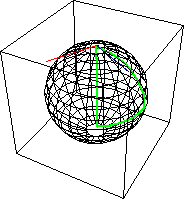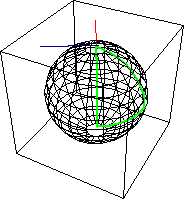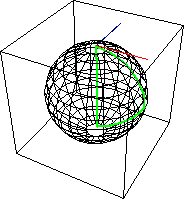
在一个 黎曼流形 上，切向量可以沿着路径通过 平行移动 来移动，这保留了 向量加法 和 标量乘法。因此，在基点 的闭环，产生 可逆线性映射 ，即 的切向量。可以将闭环一个接一个地组合，也可以通过向后追溯来反转它们。因此，由沿着闭环的 平行移动 产生的线性变换集合是一个 群，称为完整群。

由于 平行移动 保留了 黎曼度量，完整群包含在 正交群 中。此外，如果流形是 可定向的，那么它包含在 特殊正交群 中。可定向流形上的一般 黎曼度量 具有完整群 ，但对于某些特殊的度量，它可以是一个子群，在这种情况下，流形被称为具有特殊完整群。

凯勒流形 是一个 维 流形，其完整群位于 酉群 中。 卡拉比-丘流形 是一个 单连通 维流形，其完整群位于 特殊酉群 中。一个 维流形，其完整群 ，即 四元数酉群，被称为 超凯勒流形，而一个完整群为 的流形被称为 四元数凯勒流形。度量兼容的 列维-奇维塔联络 的完整群可能出现的群由 Berger 分类。非乘积、非对称 流形 的其他可能性是 李群 和 。（请注意，虽然 Berger (1955) 列出了 作为黎曼非对称完整群的可能性，但 Gray 和 Brown (1972) 排除了这种可能性。）

在 平坦流形 上，两个同伦环给出相同的线性变换。因此，完整群是 的 基本群 的 群表示。但总的来说， 的 曲率 改变了同伦环之间的 平行移动。事实上，有一个公式表示差异为曲率的积分。