主题
Search

施泰纳点

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本

存在（至少）三种不同类型的点被称为施泰纳点。

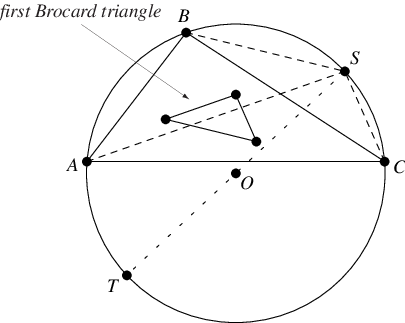
SteinerPoint

通过三角形顶点绘制的三条线，分别平行于第一 布罗卡三角形 的对应边，这三条线的 交点 S 被称为施泰纳点 (Honsberger 1995)。它位于 外接圆 上，与 塔里点 T 相对，并具有等价的 三角形中心函数。

alpha=bc(a^2-b^2)(a^2-c^2)
(1)
alpha=1/(a(b^2-c^2)).
(2)

它也位于 施泰纳外接椭圆 上。它是 Kimberling 中心 X_(99)。Kiepert 抛物线 的 布里安ション点 也是施泰纳点 (Eddy and Fritsch 1994)。类似中线点 K 是第一 布罗卡三角形 的施泰纳点 (Honsberger 1995, pp. 120-121)。施泰纳点的 西姆森线 平行于 线 OK，其中 O 是 外心，K 是 类似中线点 (Honsberger 1995, p. 121)。

第二种“施泰纳点”，更确切地称为 施泰纳曲率质心，是通过在每个顶点放置一个质量等于外角大小的质量而获得的系统的 几何质心 (Honsberger 1995, p. 120)。

PascalLines

第三种施泰纳点（Steiner 1827-1828；Lachlan 1893，pp. 115-116）产生于 帕斯卡定理 中 圆锥曲线 上的相对边三元组在 顶点 的所有排列中延伸时，产生 60 条 帕斯卡线。它们三条线的交点，共有 20 个点，被称为施泰纳点。施泰纳定理 指出，这些点是由六边形 123456、143652 和 163254 生成的，这些六边形是通过交换位置 2、4 和 6 处的顶点形成的（其中数字表示六边形顶点的选取顺序）。上面显示了内接于一般椭圆的一般六边形的 帕斯卡线 的配置，其中施泰纳点显示为填充圆圈。下面显示了左上角图形区域的放大图，说明了每条施泰纳点处三条帕斯卡线的共点。

SteinerPoints

每个施泰纳点与三个 柯克曼点 一起位于总共 20 条称为 凯莱线 的线上。施泰纳点也一次四个地位于 15 条 普吕克线 上 (Wells 1991)。20 个施泰纳点和 20 条 凯莱线 之间存在对偶关系。

另请参阅

布里安ション点, 布罗卡三角形, 凯莱线, 外接圆, 圆锥曲线, Kiepert 抛物线, 柯克曼点, 类似中线点, 帕斯卡线, 帕斯卡定理, 普吕克线, Salmon 点, 施泰纳曲率质心, 施泰纳集, 施泰纳定理, 施泰纳三元系, 塔里点

使用 Wolfram|Alpha 探索

参考文献

Casey, J. A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 66 and 329, 1893.Coolidge, J. L. A Treatise on the Geometry of the Circle and Sphere. New York: Chelsea, p. 77, 1971.Eddy, R. H. and Fritsch, R. "The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle." Math. Mag. 67, 188-205, 1994.Gallatly, W. "The Steiner and Tarry Points." §143 in The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, p. 102, 1913.Honsberger, R. "The Steiner Point and the Tarry Point." §10.5 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 119-124, 1995.Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 236-237, 281-282, 1929.Kimberling, C. "Central Points and Central Lines in the Plane of a Triangle." Math. Mag. 67, 163-187, 1994.Kimberling, C. "Steiner Point." http://faculty.evansville.edu/ck6/tcenters/class/steiner.html.Kimberling, C. "Encyclopedia of Triangle Centers: X(99)=Steiner Point." http://faculty.evansville.edu/ck6/encyclopedia/ETC.html#X99.Lachlan, R. An Elementary Treatise on Modern Pure Geometry. London: Macmillian, 1893.Neuberg, J. "Sur le point de Steiner." J. de math. spéciales, p. 29, 1886.Salmon, G. "Notes: Pascal's Theorem, Art. 267" in A Treatise on Conic Sections, 6th ed. New York: Chelsea, pp. 379-382, 1960.Steiner, J. "Questions proposées. Théorèmes sur l'hexagramum mysticum." Ann. Math. 18, 339-340, 1827-1828.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 172, 1991.

在 Wolfram|Alpha 上引用

施泰纳点

引用为

Weisstein, Eric W. “施泰纳点。” 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/SteinerPoints.html

主题分类