主题
Search

西姆森线

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
SimsonLine

西姆森线是包含从外接圆上任意点 P 到三角形的边或其延长线的垂线的垂足 P_1, P_2, 和 P_3 的线。三角形。 这条线被 Poncelet 归功于 Simson，但现在通常被称为 Wallace-Simson 线，因为它实际上并未出现在 Simson 的任何著作中（Johnson 1929, p. 137; Coxeter 和 Greitzer 1967, p. 41; de Guzmán 1999）。 上述命题的逆命题，即 三角形 DeltaABC 平面上所有点 P 的轨迹，使得从三角形三边到点的垂足共线，由 DeltaABC 的外接圆给出，有时被称为 Wallace-Simson 定理 (de Guzmán 1999)。

对于位于外接圆上的点 p:q:r，即满足

cpq+bpr+aqr=0,

西姆森线的三线方程为

(p(q+rcosA)(r+qcosA))/(sinA)alpha +(q(r+pcosB)(p+rcosB))/(sinB)beta +(r(p+qcosC)(q+pcosC))/(sinC)gamma=0

(P. Moses，私人通讯，1 月 27 日，2005 年)。

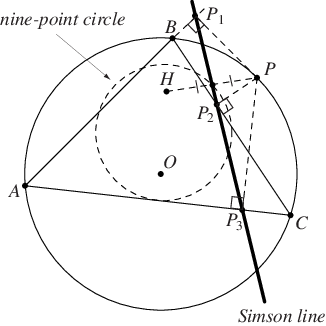
SimsonLineHP

西姆森线平分线段 HP，其中 H 是垂心 (Honsberger 1995, p. 46)。 此外，HP 的中点位于九点圆上 (Honsberger 1995, pp. 46-47)。 三角形外心上两个对点的西姆森线互相垂直，并在九点圆上相交。

两点 P 和 P^' 的西姆森线之间的角是弧 PP^' 的角的一半。 任何多边形顶点的西姆森线是通过该多边形顶点的高。 与多边形顶点相对的点的西姆森线是对应的边。 如果 T_1T_2T_3 是外接圆上的点 T 的西姆森线，则三角形 TT_1T_2 和 TA_2A_1 直接相似。

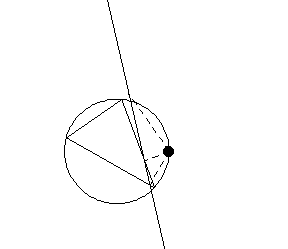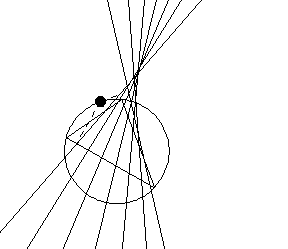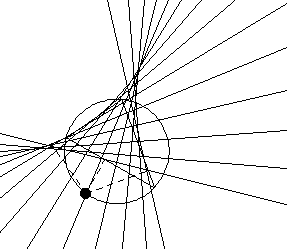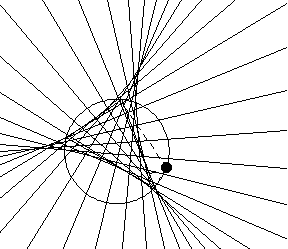
Simson line deltoid

三角形西姆森线的包络线是三角尖瓣线 (Butchart 1939; Wells 1991, pp. 155 和 230)。 三角尖瓣线的面积是外接圆面积的一半 (Wells 1991, p. 230)，并且起始三角形的第一 Morley 三角形与三角尖瓣线具有相同的方向。 三角形的每条边都与三角尖瓣线相切于一点，该点到边中点的距离等于该边截得的九点圆的弦 (Wells 1991, p. 231)。 如果线 L 是外接圆上的点 P 的西姆森线，则 P 称为 L 的西姆森线极点 (Honsberger 1995, p. 128)。

参考三角形的高是西姆森线，其西姆森线极点是参考三角形的顶点。 此外，参考三角形的边也是西姆森线，其西姆森线极点是参考三角形顶点关于其外心的反射。 另请注意，来自这些反射顶点的非平凡垂足与参考三角形的边相交于Steiner 三角尖瓣线的切点。

另请参阅

外接圆, Rigby 点, 西姆森线极点, Steiner 三角尖瓣线

此条目部分内容由 Frank Jackson 贡献

使用 探索

参考文献

Baker, H. F. An Introduction to Plane Geometry. London: Cambridge University Press, 1963.Butchart, J. H. "The Deltoid Regarded as the Envelope of Simson Lines." Amer. Math. Monthly 46, 85-86, 1939.Casey, J. A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 5th ed., rev. enl. Dublin: Hodges, Figgis, & Co., p. 164, 1888.Chou, S.-C. "Proving Elementary Geometry Theorems Using Wu's Algorithm." Contemporary Math. 29, 243-286, 1984.Coolidge, J. L. A Treatise on the Geometry of the Circle and Sphere. New York: Chelsea, p. 49, 1971.Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.Coxeter, H. S. M. and Greitzer, S. L. "Simson Lines" and "More on Simson Lines." §2.5 and 2.7 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 40-41 and 43-45, 1967.de Guzmán, M. "An Extension of the Wallace-Simson Theorem: Projecting in Arbitrary Directions." Amer. Math. Monthly 106, 574-580, 1999.Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, 1965.Durell, C. V. Modern Geometry: The Straight Line and Circle. London: Macmillan, pp. 46-48, 1928.F. Gabriel-Marie. Exercices de Géométrie. Tours, France: Maison Mame, p. 329, 1912.Gallatly, W. "The Simson Line." Ch. 4 in The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, pp. 24-36, 1913.Honsberger, R. "The Simson Line" and "Simson Lines." §5.2 and 8.4 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 43-44 and 82-83, 1995.Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 137-139, 1929.Patterson, B. C. "The Triangle: Its Deltoids and Foliates." Amer. Math. Monthly 47, 11-18, 1940.Ramler, O. J. "The Orthopole Loci of Some One-Parameter Systems of Lines Referred to a Fixed Triangle." Amer. Math. Monthly 37, 130-136, 1930.van Horn, C. E. "The Simson Quartic of a Triangle." Amer. Math. Monthly 45, 434-437, 1938.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 155 and 230-231, 1991.

在 中引用

西姆森线

引用为

Jackson, Frank 和 Weisstein, Eric W. "Simson Line." 来自 Web 资源。 https://mathworld.net.cn/SimsonLine.html

主题分类