菱形十二面体数

一种图形数，其构造方式为：一个中心立方体，每个面都附加一个四角锥，

			(1)
			(2)

其中 是一个中心立方体数， 是一个四角锥数。前几个数是 1, 15, 65, 175, 369, 671, ... (OEIS A005917)。菱形十二面体数的生成函数是

(3)

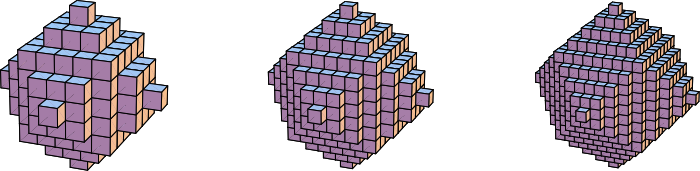
一个相关的数列是在Haüy 构造的菱形十二面体中立方体的数量，由下式给出：

(4)

对于 为奇数的情况。用 重新索引后得到：

(5)

给出的前几个值是 1, 33, 185, 553, 1233, ... (OEIS A046142)。