主题
Search

圆周率数字

下载 Mathematica Notebook下载 Wolfram Notebook

pi 的十进制展开式为

pi=3.141592653589793238462643383279502884197...
(1)

(OEIS A000796)。下表总结了一些 pi 数字的记录计算。

2061584300001999Kanada、Ushio 和 Kuroda
1.2411×10^(12)2002 年 12 月Kanada、Ushio 和 Kuroda (Peterson 2002, Kanada 2003)
5×10^(12)2012 年 8 月A. J. Yee (Yee)
10×10^(12)2012 年 8 月S. Kondo 和 A. J. Yee (Yee)
12.1×10^(12)2013 年 12 月A. J. Yee 和 S. Kondo (Yee)

自莱因德纸草书 (公元前 1500 年) 时代以来，数学家就一直致力于计算 数字 pi。Ludolph van Ceulen 一生都在计算 pi 到 35 位。尽管他生前未能发表他的结果，但它被刻在了他的墓碑上。Wells (1986, p. 48) 讨论了许多其他计算。pi 的计算也出现在星际迷航第二季剧集 "群狼" (1967) 中，在该集中，柯克舰长和斯波克先生命令计算机“计算圆周率的最后一位数字”，从而迫使计算机陷入无限循环，将一个邪恶实体（由纯能量组成，以恐惧为食）赶出了星舰进取号的计算机。

Al-Kāshi of Samarkand 计算了 2pi 的 六十进制 数字为

2pi=6.(16)(59)(28)(01)(34)(51)(46)(14)(50)_(60)...
(2)

(OEIS A091649)，使用 3·2^(28)-边形，该值精确到小数点后 17 位 (Borwein and Bailey 2003, p. 107)。

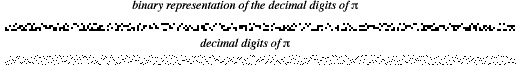
Pi digits

上面说明了 pi 的十进制数字的二进制表示（上图）和 pi 的十进制表示（下图）。

Pi digits mod 2

上面（左图）显示了 pi 的前 1600 位十进制数字的图（mod 2），右图显示了 22/7 的相应图。这里，白色表示偶数数字，黑色表示奇数数字 (Pickover 2002, p. 285)。

Spigot (Rabinowitz and Wagon 1995; Arndt and Haenel 2001; Borwein and Bailey 2003, pp. 140-141) 和基数 16 数字提取算法 (BBP 公式) 是已知的 pi 算法。一个值得注意的递归公式被猜想可以给出 n 位 十六进制 数字 pi-3，由 d_n=|_16x_n_| 给出，其中 |_x_| 是向下取整函数，

x_n=frac(16x_(n-1)+(120n^2-89n+16)/(512n^4-1024n^3+712n^2-206n-21)),
(3)

frac(x) 是 小数部分，x_0=0 (Borwein and Bailey 2003, Ch. 4; Bailey et al. 2007, pp. 22-23)。

极限 圆周率公式

lim_(n->infty)((2(-1)^(n+1)(2n)!)/(2^(2n)B_(2n)))^(1/(2n))=pi,
(4)

和

lim_(n->infty)((2(-1)^(n+1)(2n)!)/(2^(2n)B_(2n)(1-2^(-n))(1-3^(-n))(1-5^(-n))(1-7^(-n))))^(1/(2n))=pi,
(5)

其中 B_n 是 伯努利数 (Plouffe 2022)，可以用作 pi (以及 pi^n) 的 数字提取算法。特别是，令

pi_n=((2(-1)^(n+1)(2n)!)/(2^(2n)B_(2n)(1-2^(-n))(1-3^(-n))(1-5^(-n))(1-7^(-n))))^(1/(2n)),
(6)

对于 n>=3，n 位数字在小数点右侧 pi 由下式给出

d_n=int(10frac(10^(n-1)pi_(n-1)))
(7)

其中 int(x) 是 整数部分，frac(x) 是 小数部分。可以使用以下公式获得类似的公式

lim_(n->infty)((2^(2n+2)(-1)^n(2n)!)/(E_(2n)))^(1/(2n+1))=pi
(8)

和

lim_(n->infty)((2^(2n+2)(-1)^n(2n)!)/(E_(2n))(1-1/(3^(2n+1))))^(1/(2n+1))=pi,
(9)

其中 E_n 是 欧拉数，这给出了一个基数 9（或二进制）数字提取算法 (Plouffe 2022)。也可以为 pi^2 获得相关的极限和公式 (Plouffe 2022)。

圆周率素数，即 pi-常数素数 出现在 2, 6, 38, 16208, 47577, 78073, 613373, ... (OEIS A060421) 十进制数字处。

兽数 666 出现在 pi-3 的小数位 2440, 3151, 4000, 4435, 5403, 6840, (OEIS A083625)。连续 n 个 6 的首次出现位置是 7, 117, 2440, 21880, 48439, 252499, 8209165, 55616210, 45681781, ... (OEIS A096760)，而 n 个（或更多）连续 6 的首次出现位置是 7, 117, 2440, 21880, 48439, 252499, 8209165, 45681781, 45681781, ... (OEIS A050285)。

数字 314159 出现在位置 176451, 1259351, 1761051, 6467324, 6518294, 9753731, 9973760, ... （更正了 Pickover 1995）。

序列 0123456789 出现在数字 17387594880, 26852899245, 30243957439, 34549153953, 41952536161, 和 43289964000 (OEIS A101815; cf. Wells 1986, pp. 51-52) 开头。

序列 9876543210 出现在数字 21981157633, 29832636867, 39232573648, 42140457481, 和 43065796214 (OEIS A101816) 开头。

序列 27182818284 ( e 的前几位数字) 出现在数字 45111908393 开头 (另请参见 Pickover 序列)。

对于 1/pi 也存在有趣的模式。0123456789 出现在 6214876462，9876543210 出现在 15603388145 和 51507034812，而 999999999999 出现在 12479021132 的 1/pi。

十进制展开式中 pi 的 n=0, 1, 2, ... 的首次出现起始位置（包括初始 3 并将其计为第一个数字）是 33, 2, 7, 1, 3, 5, 8, 14, ... (OEIS A032445)。

扫描 pi 的十进制展开式，直到所有 n 位数字都出现过，最后出现的 1 位、2 位、... 位数字是 0, 68, 483, 6716, 33394, 569540, ... (OEIS A032510)，它们在数字 33, 607, 8556, 99850, 1369565, ... (OEIS A080597) 处结束。

一个将 pi 与 兽数 666 联系起来的奇特之处在于将 pi 的前三个六位数相加。首先，请注意

141592+653589+793238=1588419.
(10)

现在，跳过 15 个十进制位，并注意总和重复为

3.141592 653589 793238 462643383279502^(︷)^(15) 88419 71693
(11)

（个人通讯，P. Olivera，2005 年 8 月 11 日；Olivera）。

不知道 pi 是否是 正规数 (Wagon 1985, Bailey and Crandall 2001)，尽管前 3000 万个 数字 非常 均匀分布 (Bailey 1988)。

对于前 10^n 个 数字 pi-3 (Kanada 2003)，发现了以下十进制数字 d 的分布。它没有显示出与 均匀分布 的统计 显著 偏差。

nOEIS23456789101112
0A0992918939689999999599994409999922999939429999679951000010475099999485134
1A09929281161026101379975899933310002475999973341000037790999993763199999945664
2A0992931210310219908100026100030610001092100002410100001727110000026432100000480057
3A0992941110297410025100229999964999844299986911999976483999991239699999787805
4A09929510931012997110023010010931000386310001195899993768810000032702100000357857
5A09929689710461002610035910004669993478999988851000007928999996366199999671008
6A099297994102110029995489993379999417100010387999985731999982408899999807503
7A0992988959701002599800100020799996109999606110000413301000008453099999818723
8A099299121019489978999859998141000218010000183999999177210000157175100000791469
9A0993001410610149902100106100004099995211000002731000036012999995663599999854780

下表给出了数字 d 出现 n 次的首次几个位置。由对角线（加上任何 10 个 10 等形式的项）给出的序列 1, 135, 1698, 54525, 24466, 252499, 3346228, 46663520, 564665206, ... (OEIS A061073) 被称为 Earls 序列 (Pickover 2002, p. 339)。序列 999999 出现在十进制位 762 (有时称为 费曼点；Wells 1986, p. 51)，并继续为 9999998，这是前一百万个十进制位中任何七位数字的最大值。

dOEIS1 位、2 位、...d 字符串首次出现在
0A05027932, 307, 601, 13390, 17534, 1699927, ...
1A0351171, 94, 153, 12700, 32788, 255945, ...
2A0502816, 135, 1735, 4902, 65260, 963024, ...
3A0502829, 24, 1698, 28467, 28467, 710100, ...
4A0502832, 59, 2707, 54525, 808650, 828499, ...
5A0502844, 130, 177, 24466, 24466, 244453, ...
6A0502857, 117, 2440, 21880, 48439, 252499, ...
7A05028613, 559, 1589, 1589, 162248, 399579, ...
8A05028711, 34, 4751, 4751, 213245, 222299, ...
9A0489405, 44, 762, 762, 762, 762, 1722776, ...

Knuth (2024, p. 18) 指出了 优美的圆周率路径 中 pi 的前 30 位数字的“奇迹般”出现，即 美国本土图 的特定 优美标记。

另请参见

常数数字扫描, 常数素数, Earls 序列, 圆周率, 圆周率近似值, 圆周率连分数, 圆周率公式, Pickover 序列

使用 Wolfram|Alpha 探索

参考文献

Adamchik, V. and Wagon, S. "pi 的简单公式。" Amer. Math. Monthly 104, 852-855, 1997。Anderson, D. "Pi-Search 页面。" http://www.angio.net/pi/piquery。Arndt, J. and Haenel, C. Pi--释放，第二版。 柏林：Springer-Verlag, 2001。Bailey, D. H. "使用 Borwein 的四次收敛算法计算 pi 到 29360000 位十进制数字。" Math. Comput. 50, 283-296, 1988。Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. 行动中的实验数学。 Wellesley, MA: A K Peters, 2007。Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "关于各种多对数常数的快速计算。" Math. Comput. 66, 903-913, 1997。Bailey, D. H. and Crandall, R. E. "关于基本常数展开式的随机特征。" Exper. Math. 10, 175-190, 2001. http://www.nersc.gov/~dhbailey/dhbpapers/baicran.pdf。Borwein, J. M. "谈论圆周率。" http://www.cecm.sfu.ca/personal/jborwein/pi_cover.html。Borwein, J. and Bailey, D. 实验数学：21 世纪的合理推理。 Wellesley, MA: A K Peters, 2003。Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "拉马努金、模方程和圆周率的近似值，或如何计算十亿位圆周率。" Amer. Math. Monthly 96, 201-219, 1989。Caldwell, C. K. and Dubner, H. "圆周率中的素数。" J. Recr. Math. 29, 282-289, 1998。Gibbs, W. W. "圆周率的数字切片。纯数学的新方法：实验性。" Sci. Amer. 288, 23-24, 2003 年 5 月。Gourdon, X. and Sebah, P. "PiFast：计算圆周率的最快程序。" http://numbers.computation.free.fr/Constants/PiProgram/pifast.html。Kanada, Y. "圆周率的新世界纪录：515 亿位十进制数字。" http://www.cecm.sfu.ca/personal/jborwein/Kanada_50b.html。更新链接Kanada, Y. "我们的最新记录。" 1999 年 9 月 20 日。 ftp://www.cc.u-tokyo.ac.jp/README.our_latest_recordKanada, Y. "圆周率十进制数字的样本数字。" 2003 年 1 月 18 日。 http://www.super-computing.org/pi-decimal_current.html。Knuth, D. E. §7.2.2.3 in 计算机程序设计艺术，第 4 卷。 预先印制本 7A，2024 年 12 月 5 日。Le Lionnais, F. Les nombres remarquables. 巴黎：Hermann, pp. 22 和 50, 1983。National Energy Research Scientific Computing Center. "搜索 pi。" http://pi.nersc.gov/。Olivera, P. "关于多年前我在寻找模式和序列时如何发现圆周率中一个奇特模式的事件的简要描述。" http://www.geocities.com/pi_curiosity/englishstory.html。Peterson, I. "选择一个数字，任何数字。" Sci. News Online, 1998 年 2 月 28 日。 http://www.sciencenews.org/sn_arc98/2_28_98/mathland.htm。Peterson, I. "数十亿位的圆周率。" Sci. News 156, 255, 1999 年 10 月 16 日。Peterson, I. "时尚的圆周率。" Sci. News 160, 136-137, 2001 年 9 月 1 日。 http://www.sciencenews.org/20010901/bob9.asp。Peterson, I. "对圆周率的热情。" In 数学之旅：从超现实数到魔术圈。 Washington, DC: Math. Assoc. Amer., 2001。Peterson, I. "MathTrek：万亿位的圆周率。" 2002 年 12 月 14 日。 http://www.sciencenews.org/20021214/mathtrek.asp。Pickover, C. A. 无限之钥。 纽约：Wiley, p. 62, 1995。Pickover, C. A. 奥兹数学：来自边缘之外的智力体操。 纽约：Cambridge University Press, pp. 284-285, 2002。Plouffe, S. "当前常数计算记录表。" http://pi.lacim.uqam.ca/eng/records_en.html。Plouffe, S. "n 位十进制数字或 pi 和 pi^n 二进制的公式。" https://arxiv.org/abs/2201.12601。 2022 年 1 月 29 日。Rabinowitz, S. and Wagon, S. "pi 数字的 Spigot 算法。" Amer. Math. Monthly 102, 195-203, 1995。Sloane, N. J. A. 序列 A000796/M2218, A032150, A032445, A035117, A036903, A036974, A037000, A037001, A037002, A037003, A037004, A037005, A037006, A037007, A037008, A048940, A050201, A050202, A050203, A050208, A050209, A050215, A050222, A050230, A050238, A050245, A050254, A050263, A050272, A050279, A050281, A050282, A050283, A050284, A050285, A050286, A050287, A060421, A061073, A080597, A083625, A091649, A096760, A099291, A099292, A099293, A099294, A099295, A099296, A099297, A099298, A099299, A099300, A101815, 和 A101816 在 "整数序列在线百科全书" 中。Smith, H. J. "计算圆周率。" http://www.geocities.com/hjsmithh/Pi.html。Wagon, S. "pi 是正规数吗？" Math. Intel. 7, 65-67, 1985。Wells, D. 企鹅好奇和有趣的数字词典。 Middlesex, England: Penguin Books, p. 46, 1986。Wrench, J. W. Jr. "pi 的扩展十进制近似值的演变。" Math. Teacher 53, 644-650, 1960。Yee, A. J. "y-cruncher - 多线程圆周率程序。" http://www.numberworld.org/y-cruncher/。

请引用为

Weisstein, Eric W. "圆周率数字。" 来自 MathWorld--一个 Wolfram Web 资源。 https://mathworld.net.cn/PiDigits.html

主题分类