整数部分 -- 来自 Wolfram MathWorld

整数部分

函数给出的整数部分。在许多计算机语言中，该函数表示为int(x)。它与 floor 函数和 ceiling 函数和相关，关系如下

$int(x)={|_x_| for x>=0; [x] for x<0.$

(1)

整数部分函数满足

(2)

并在 Wolfram 语言中实现为IntegerPart[x]。此定义的选择使得 $int(x)+frac(x)=x$ ，其中 $frac(x)$ 是小数部分。虽然 Spanier 和 Oldham (1987) 使用与 Wolfram 语言中相同的定义，但他们只是非常简要地提到了这个公式，然后表示它将不再被进一步使用。Graham et al. (1994) 以及可能大多数其他数学家，将术语“整数”部分与 floor 函数交替使用。

	最小值	最大值
Re
Im

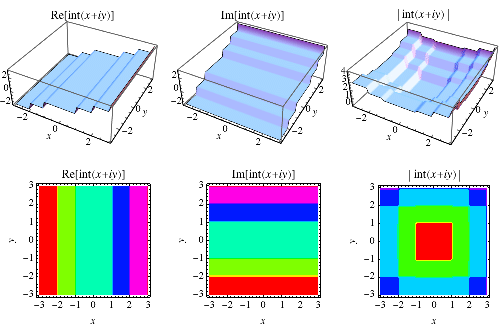整数部分函数也可以扩展到复平面，如上图所示。

由于关于小数部分/值和整数部分/值的用法可能会令人困惑，下表总结了使用的名称和符号。这里，S&O 表示 Spanier 和 Oldham (1987)。

符号	名称	S&O	Graham et al.	Wolfram 语言
	ceiling 函数	--	ceiling，最小整数	`Ceiling`[x]
	同余	--	--	`Mod`[m, n]
	floor 函数		floor，最大整数，整数部分	`Floor`[x]
	小数值	$frac(x)$	小数部分或	`SawtoothWave`[x]
	小数部分		无名称	`FractionalPart`[x]
	整数部分		无名称	`IntegerPart`[x]
	最近整数函数	--	--	`Round`[x]
$m\n$	商	--	--	`Quotient`[m, n]

参考文献