七边形三角形

由正 七边形 的三个顶点形成的唯一（模旋转）不等边三角形，其顶角为 、 和 。 有许多神奇的公式将七边形三角形的边和角联系起来（Bankoff 和 Garfunkel 1973）。

三角形的 面积 为

其中 是三角形的 外接圆半径。 七边形三角形的边长的平方和等于 （Bankoff 和 Garfunkel 1973）。 内切圆半径 与 外接圆半径 的比率 由以下方程的正根给出

边长满足

（Bankoff 和 Garfunkel 1973）和

后者可以通过将 托勒密定理 应用于边长为 、 、 和 ，对角线为 和 的四边形，然后除以 来轻松证明（I. Larrosa Cañestro，私人通讯，2006 年 4 月 23 日）。

布罗卡角 满足

并且 旁切圆半径 等于 的 九点圆 的半径。

是另外两条边的 调和平均数 的一半，

对于变量的所有排列组合等式都成立（Bankoff 和 Garfunkel 1973）。 此外，

如果 、 和 是高，则

如果 、 和 是高的垂足，则

等等（Bankoff 和 Garfunkel 1973）。 角 和 的内角平分线等于邻边之差，角 的外角平分线等于邻边之和。

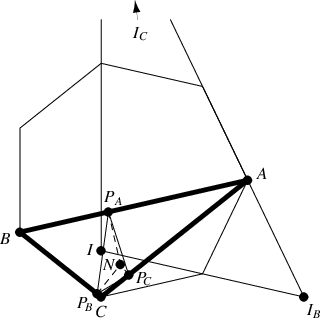
连接七边形三角形的角平分线的垂足的三角形 是 等腰三角形，其中 。

垂心三角形 和 中线三角形 是全等且透视的。 此外，两者都类似于 、 关于 九点中心 的 垂足三角形 以及由 内心 和外角平分线 和 形成的三角形 （Bankoff 和 Garfunkel 1973）。 三角形 也类似于这些三角形。

还有大量有趣的三角恒等式与七边形三角形的角度有关

（Bankoff 和 Garfunkel 1973）。

此外，

最后，七边形三角形满足以下其他性质

1. 第一个 布罗卡点 对应于 九点中心，第二个 布罗卡点 位于 九点圆 上。

2. ，其中 是 外心， 是 垂心， 是 外接圆半径。

3. ，其中 是 内心， 是 内切圆半径。

4. 从 垂心 到七边形三角形的 外接圆 的两条切线互相垂直。

5. 切线三角形 的 外接圆 的中心与 关于 的对称点重合。

6. 从 出发的高是角 的内角平分线长度的一半。