最大公约数

最大公约数，有时也称为最高公约数 (Hardy and Wright 1979, p. 20)，是两个正整数 和 最大的共同约数，即 和 都能被它整除。例如，，，和 。最大公约数 也可以定义为三个或更多正整数的最大公约数，即它们共有的最大约数。最大公约数为 1 的两个或多个正整数被称为彼此互质，通常简称为“互质”。

各种符号约定总结在下表中。

符号	来源
	本作品，Zwillinger (1996, p. 91), Råde and Westergren (2004, p. 54)
	Gellert et al. (1989, p. 25), D'Angelo and West (1990, p. 13), Graham et al. (1990, p. 103), Bressoud and Wagon (2000, p. 7), Yan (2002, p. 30), Bronshtein et al. (2007, pp. 323-324), Wolfram Language
g.c.d.	Andrews 1994, p. 22

, , ... 的最大公约数在 Wolfram Language 中实现为GCD[a, b, ...].

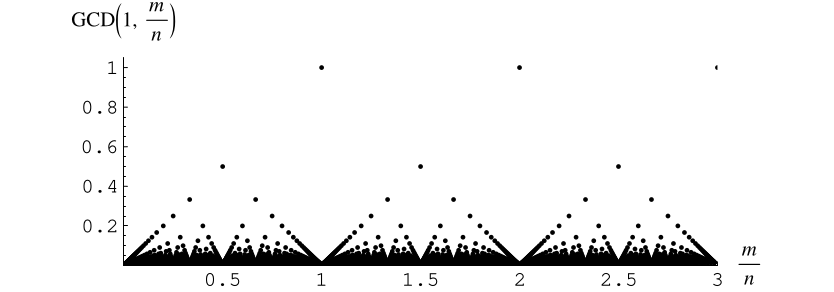
上图显示了 与有理数 的关系。这里， 是最大的有理数 ，对于它，所有的 都是整数。很容易看出，如果 ，其中 ，那么 。此外，如果通过将 扩展为当 是无理数时，其值等于 0，则得到的函数在无理数处连续，在有理数处不连续，并且在任何有限区间上的黎曼积分等于 0。

以上图表显示了 在 -平面中的一些可视化表示。左图是简单的 ，中间的图是 的二维离散傅里叶变换的绝对值 (Trott 2004, pp. 25-26)，右图是 变换的绝对值。

如果 是 和 的最大公约数，那么 是满足以下条件的最大可能整数

			(1)
			(2)

其中 和 是正整数。

欧几里得算法可以用来求两个整数的最大公约数，并找到整数 和 使得

(3)

这个概念也可以推广到比整数 更一般的环。然而，即使对于欧几里得环，两个环元素的 GCD 的概念与环的两个理想的 GCD 概念也不同。当研究除 以外的环（例如多个变量的多项式环）时，这有时会成为混淆的来源。

为了计算 GCD，写出 和 的素因数分解，

			(4)
			(5)

其中 s 是 和 的所有素因子，并且如果 没有在一个因式分解中出现，则相应的指数取为 0。那么最大公约数 由下式给出

(6)

其中 min 表示最小值。例如，考虑 。

			(7)
			(8)

所以

(9)

GCD 是可分配的

(10)

(11)

且是结合性的

			(12)
			(13)
			(14)

如果 且 ，则

			(15)
			(16)

所以 。GCD 也是幂等的

(17)

交换律

(18)

并满足吸收律

(19)

对于正奇数 和 ，收敛到 的递归方程由下式给出

(20)

其中 和 ，其中 是 在 中的最大整除指数 (Stehlé and Zimmerman 2004)。上图显示了奇数 收敛所需的迭代次数。

随机选择的两个整数互质的概率为 ，其中 是黎曼 zeta 函数。Polezzi (1997) 观察到 ，其中 是平面上连接向量 (0, 0) 和 的直线上的格点数（不包括 本身）。这个观察结果与获得互质整数的概率密切相关，也与既约分数 的几何解释有关，即作为穿过格点的字符串，端点为 (1,0) 和 。它压在 上的钉子给出了 的交替收敛项，是 的连分数，而其他收敛项是从它压在钉子上获得的，初始端点为 (0, 1)。

Knuth 证明了

(21)