大二十面体

大二十面体，不要与大icosidodecahedron或大icosicosidodecahedron混淆，是开普勒-泊松多面体，其对偶是大星形十二面体。它也是 Maeder 索引为 53 (Maeder 1997)、Wenninger 索引为 41 (Wenninger 1989)、Coxeter 索引为 69 (Coxeteret al.1954) 和 Har'El 索引为 58 (Har'El 1993) 的均匀多面体。它具有Schläfli 符号 和Wythoff 符号 。

大二十面体可以从边长为单位长度的二十面体构建，方法是取 20 组顶点，这些顶点彼此间隔距离 ，即黄金比例。因此，该实体由 20 个等边三角形组成。它们的排列方式的对称性使得所得实体包含 12 个五角星。

最容易构建大二十面体的方法是，从相应的网格（左上图）构建一个“压扁的”十二面体（右上图）。然后，使用左下图所示的网格，构建 12 个五角星锥体（中下图），并将它们贴在凹坑中（右下图）。Cundy 和 Rollett (1989, pp. 98-99) 给出了这种构建方法。如果十二面体的边长为单位长度，则五角星锥体的高度（在十二面体面之上）由求解五角锥体的边长方程给出

(1)

其中 ，得到

(2)

然后，从十二面体的中心到锥体顶点的距离由下式给出

(3)

其中 是十二面体的内半径。

大二十面体的骨架与二十面体图同构。

上面的插图显示了一个大二十面体的纸雕。模型的每个面平面都是不同的颜色，但成对的平行面使用相同的颜色。该模型由 180 个部件制成。

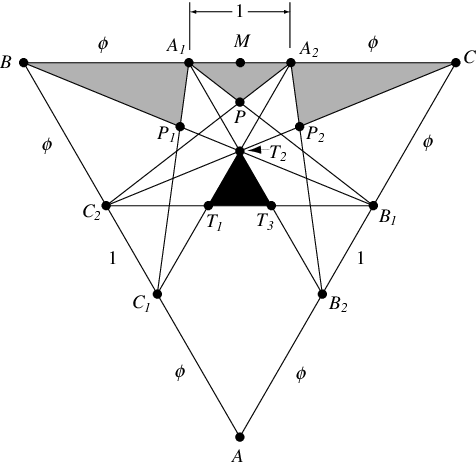
五角星锥体的尺寸可以通过检查大二十面体的三角形截面来确定。在这个三角形中，每条边都按比例 分割，并如图所示绘制线条。然后，左侧和右侧的浅色阴影部分对应于两个锥体的侧面，中心阴影部分是前两个锥体之间锥体的“唇”。此外，图中的填充部分对应于刻在大二十面体中的二十面体的一个面。在上面图形的符号中，

			(4)
			(5)
			(6)
			(7)
			(8)

由边长为单位长度的十二面体构建的大二十面体的边长（其中边被解释为在面平面相交处断开）由下式给出

			(9)
			(10)
			(11)
			(12)

它的外接球半径是

(13)

然后表面积和体积是

			(14)
			(15)
			(16)

大二十面体的凸包是一个正二十面体，二十面体的对偶是十二面体，所以大二十面体的对偶是十二面体星状体之一 (Wenninger 1983, p. 40)