令参考三角形 的内和外 索迪三角形 分别表示为
和
。类似地,令
和
的 切线三角形 分别表示为
和
。那么,内(分别为外)Rigby 点 Ri (分别为
)是
和
(分别为
和
)的 透视中心 (Oldknow 1996)。Rigby 点位于 索迪线 上。它们具有 三角形中心函数
|
(1)
| |||
|
(2)
|
分别是 Kimberling 中心 和
。
Honsberger (1995) 定义了一个不同的点,他称之为 “Rigby point” 。令
为给定三角形
的 外接圆 的任意 弦,并令
为关于 三角形
且 垂直 于
的 西姆森线
的 西姆森线极点。那么结果也表明
和
。此外,关于
,也有
、
和
。
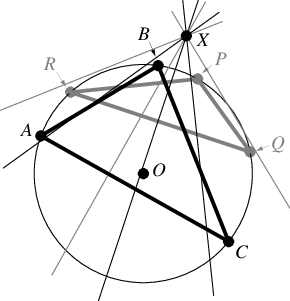
由于这些非凡的事实,可以证明关于 的 西姆森线
、
和
交于 Rigby point
。此外,关于
的 西姆森线
、
和
也交于
,并且
是
的 垂极,也是
的 垂极。最后,
是
和
的 垂心 的 中点 (Honsberger 1996, p. 136)。