球谐函数  是 拉普拉斯方程 在 球坐标系 中当不存在方位角对称性时的解的角度部分。在识别所使用的符号约定方面必须谨慎。在本条目中,
是 拉普拉斯方程 在 球坐标系 中当不存在方位角对称性时的解的角度部分。在识别所使用的符号约定方面必须谨慎。在本条目中, 被视为极(余纬)坐标,其中
被视为极(余纬)坐标,其中 ![theta in [0,pi]](/images/equations/SphericalHarmonic/Inline3.svg) ,而
,而  被视为方位角(经度)坐标,其中
被视为方位角(经度)坐标,其中  。这是物理学中常用的约定,正如 Arfken (1985) 和 Wolfram 语言 所描述的那样(在数学文献中,
。这是物理学中常用的约定,正如 Arfken (1985) 和 Wolfram 语言 所描述的那样(在数学文献中, 通常表示经度坐标,而
通常表示经度坐标,而  表示余纬坐标)。球谐函数在 Wolfram 语言 中实现为SphericalHarmonicY[l, m, theta, phi].
表示余纬坐标)。球谐函数在 Wolfram 语言 中实现为SphericalHarmonicY[l, m, theta, phi].
球谐函数满足 球谐微分方程,该方程由 拉普拉斯方程 在 球坐标系 中的角度部分给出。在这个方程中写入  得到
得到
 |
(1)
|
乘以  得到
得到
![[(sintheta)/(Theta(theta))d/(dtheta)(sintheta(dTheta)/(dtheta))+l(l+1)sin^2theta]+1/(Phi(phi))(d^2Phi(phi))/(dphi^2)=0.](/images/equations/SphericalHarmonic/NumberedEquation2.svg) |
(2)
|
使用 分离变量法,通过将  相关部分等同于常数,得到
相关部分等同于常数,得到
 |
(3)
|
其解为
 |
(4)
|
将 (3) 代入 (2) 得到  相关部分的方程,其解为
相关部分的方程,其解为
 |
(5)
|
其中  ,
,  , ..., 0, ...,
, ..., 0, ...,  ,
,  且
且  是一个 缔合勒让德多项式。然后通过组合
是一个 缔合勒让德多项式。然后通过组合  和
和  定义球谐函数,
定义球谐函数,
 |
(6)
|
其中选择归一化使得
 |
(7)
|
(Arfken 1985, p. 681)。这里, 表示 复共轭,而
表示 复共轭,而  是 克罗内克 delta。有时(例如,Arfken 1985),Condon-Shortley 相位
是 克罗内克 delta。有时(例如,Arfken 1985),Condon-Shortley 相位  被预先添加到球谐函数的定义中。
被预先添加到球谐函数的定义中。
球谐函数有时会分为它们的 实部 和 虚部,
 |
(8)
|
 |
(9)
|
球谐函数服从
其中  是 勒让德多项式。
是 勒让德多项式。
球谐函数的积分由下式给出
 |
(13)
|
其中  是一个 维格纳 3j 符号(它与 克莱布施-戈尔丹系数 相关)。特殊情况包括
是一个 维格纳 3j 符号(它与 克莱布施-戈尔丹系数 相关)。特殊情况包括
(Arfken 1985, p. 700)。
以上图示显示了  (顶部),
(顶部),![R[Y_l^m(theta,phi)]^2](/images/equations/SphericalHarmonic/Inline46.svg) (左下),和
(左下),和 ![I[Y_l^m(theta,phi)]^2](/images/equations/SphericalHarmonic/Inline47.svg) (右下)。前几个球谐函数是
(右下)。前几个球谐函数是
用 笛卡尔坐标系 表示,
因此
带谐函数 被定义为 形式为
 |
(43)
|
扇谐函数 是 形式为
 |
(44)
|
 |
(45)
|
对于  。节谐函数 是 形式为
。节谐函数 是 形式为
 |
(46)
|
 |
(47)
|
另请参阅
缔合勒让德多项式,
Condon-Shortley 相位,
相关系数,
拉普拉斯级数,
节谐函数,
实体谐函数,
球谐函数加法定理,
球谐微分方程,
球谐函数闭包关系,
面谐函数,
扇谐函数,
矢量球谐函数,
带谐函数
相关 Wolfram 网站
http://functions.wolfram.com/Polynomials/SphericalHarmonicY/,
http://functions.wolfram.com/HypergeometricFunctions/SphericalHarmonicYGeneral/
使用 探索
参考文献
Abbott, P. "2. 薛定谔方程。" 计算物理 2 讲义。 http://physics.uwa.edu.au/pub/Computational/CP2/2.Schroedinger.nb.Arfken, G. "球谐函数" 和 "三个球谐函数乘积的积分。" §12.6 和 12.9 在 物理学家的数学方法,第 3 版。 奥兰多,佛罗里达州:学术出版社,pp. 680-685 和 698-700, 1985.Byerly, W. E. "球谐函数。" 第 6 章 在 傅里叶级数、球谐函数、柱谐函数和椭球谐函数的基本论著,附带在数学物理问题中的应用。 纽约:多佛出版社,pp. 195-218, 1959.Ferrers, N. M. 关于球谐函数及与其相关主题的初等论著。 伦敦:麦克米伦出版社,1877.Groemer, H. 傅里叶级数和球谐函数的几何应用。 纽约:剑桥大学出版社,1996.Hobson, E. W. 球谐函数和椭球谐函数理论。 纽约:切尔西出版社,1955.Kalf, H. "关于任意维度函数按球谐函数展开。" Bull. Belg. Math. Soc. Simon Stevin 2, 361-380, 1995.MacRobert, T. M. 和 Sneddon, I. N. 球谐函数:调和函数的初等论著,附带应用,第 3 版修订版。 牛津,英格兰:珀加蒙出版社,1967.Normand, J. M. 李群:量子力学中的旋转。 阿姆斯特丹,荷兰:北荷兰,1980.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; 和 Vetterling, W. T. "球谐函数。" §6.8 在 FORTRAN 数值食谱:科学计算的艺术,第 2 版。 剑桥,英格兰:剑桥大学出版社,pp. 246-248, 1992.Sansone, G. "调和多项式和球谐函数"、"球谐函数的积分性质和勒让德多项式的加法定理" 以及 "关于平方可积函数的球谐函数的完备性。" §3.18-3.20 在 正交函数,修订英文版。 纽约:多佛出版社,pp. 253-272, 1991.Sternberg, W. 和 Smith, T. L. 势论和球谐函数理论,第 2 版。 多伦多:多伦多大学出版社,1946.Wang, J.; Abbott, P.; 和 Williams, J. "原子轨道的可视化。" http://physics.uwa.edu.au/pub/Orbitals.Weisstein, E. W. "关于球谐函数的书籍。" http://www.ericweisstein.com/encyclopedias/books/SphericalHarmonics.html.Whittaker, E. T. 和 Watson, G. N. "涉及勒让德函数的拉普拉斯方程的解" 和 "满足球体表面上指定边界条件的拉普拉斯方程的解。" §18.31 和 18.4 在 现代分析教程,第 4 版。 剑桥,英格兰:剑桥大学出版社,pp. 391-395, 1990.Zwillinger, D. 微分方程手册,第 3 版。 波士顿,马萨诸塞州:学术出版社,p. 129, 1997.在 中引用
球谐函数
请引用本文为
Weisstein, Eric W. "球谐函数。" 来源 Web 资源。 https://mathworld.net.cn/SphericalHarmonic.html
主题分类
是 拉普拉斯方程 在 球坐标系 中当不存在方位角对称性时的解的角度部分。在识别所使用的符号约定方面必须谨慎。在本条目中,
被视为极(余纬)坐标,其中
,而
被视为方位角(经度)坐标,其中
。这是物理学中常用的约定,正如 Arfken (1985) 和 Wolfram 语言 所描述的那样(在数学文献中,
通常表示经度坐标,而
表示余纬坐标)。球谐函数在 Wolfram 语言 中实现为SphericalHarmonicY[l, m, theta, phi].
得到
得到
相关部分等同于常数,得到
,
, ..., 0, ...,
,
且
是一个 缔合勒让德多项式。然后通过组合
和
定义球谐函数,


表示 复共轭,而
是 克罗内克 delta。有时(例如,Arfken 1985),Condon-Shortley 相位
被预先添加到球谐函数的定义中。




是 勒让德多项式。

是一个 维格纳 3j 符号(它与 克莱布施-戈尔丹系数 相关)。特殊情况包括



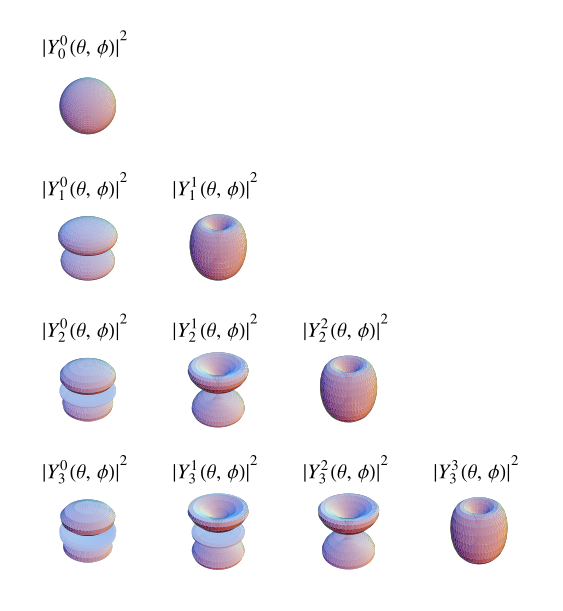
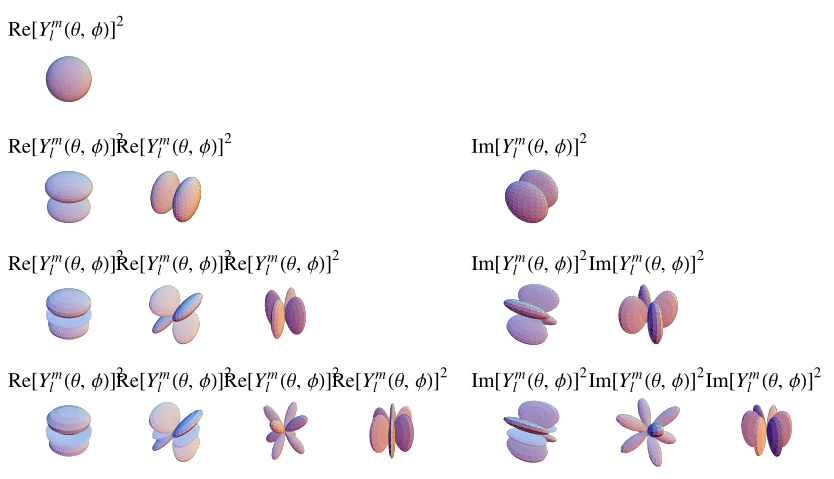
(顶部),
(左下),和
(右下)。前几个球谐函数是




















