莫比乌斯带,也称为扭曲柱面(Henle 1994,第 110 页),是一种单侧不可定向曲面,通过将一个闭合带切成一个条状,将由此产生的两个端部之一扭转半圈,然后重新连接两个端部而获得(右图;Gray 1997,第 322-323 页)。以他的名字命名的带是由莫比乌斯在 1858 年发明的,尽管它是由 Listing 独立发现的,Listing 发表了它,而莫比乌斯没有发表(Derbyshire 2004,第 381 页)。与柱面一样,它不是真正的曲面,而是一个带边界的曲面(Henle 1994,第 110 页)。
莫比乌斯带具有欧拉示性数  (Dodson and Parker 1997, p. 125)。
(Dodson and Parker 1997, p. 125)。
根据 Madachy (1979) 的说法,B. F. Goodrich 公司获得了一种莫比乌斯带形式的传送带的专利,这种传送带的寿命是传统传送带的两倍。M. C. 埃舍尔喜欢描绘莫比乌斯带,它们出现在他的木刻作品《莫比乌斯带 I》和《莫比乌斯带 II(红蚂蚁)》中(Bool 等人 1982,第 324 页;Forty 2003,图版 70)。
半宽为  的莫比乌斯带,其中圆心半径为
的莫比乌斯带,其中圆心半径为  且高度为
且高度为  可以参数化表示为
可以参数化表示为
对于 ![s in [-w,w]](/images/equations/MoebiusStrip/Inline14.svg) 和
和  。在这种参数化中,莫比乌斯带因此是一个三次曲面,其方程为
。在这种参数化中,莫比乌斯带因此是一个三次曲面,其方程为
 |
(4)
|
上面的图示显示了沿着莫比乌斯带长度方向相互啮合的转动齿轮(M. Trott,私人通讯,2001)。
这个曲面的第一基本形式的系数是
第二基本形式的系数是
面积元素是
 |
(11)
|
并且高斯和平均曲率是
莫比乌斯带的周长是通过积分复杂函数给出的
![ds=sqrt(x^('2)+y^('2))
=[1/(16)w^4cos^4(1/2t)+{[R+wcos(1/2t)]cost-1/2wsin(1/2t)sint}^4+{Rsint+1/4w[sin(1/2t)+3sin(3/2t)]}^4]^(1/2)](/images/equations/MoebiusStrip/NumberedEquation3.svg) |
(14)
|
从 0 到  的积分,遗憾的是无法以闭合形式完成。请注意,虽然曲面在
的积分,遗憾的是无法以闭合形式完成。请注意,虽然曲面在  处闭合,但这对应于底部边缘与顶部边缘连接,如上图所示,因此必须额外遍历
处闭合,但这对应于底部边缘与顶部边缘连接,如上图所示,因此必须额外遍历  才能构成边界边缘的整个弧长。
才能构成边界边缘的整个弧长。
切割莫比乌斯带,给它额外的扭曲,然后重新连接两端会产生意想不到的图形,称为并合环(Listing 和 Tait 1847,Ball 和 Coxeter 1987),如下表所示。
| 半扭曲 | 切割 | 分段 | 结果 |
| 1 | 1 | 2 | 1 条带,长度 2 |
| 1 | 1 | 3 | 1 条带,长度 2 |
| | | 1 条莫比乌斯带,长度 1 |
| 1 | 2 | 4 | 2 条带,长度 2 |
| 1 | 2 | 5 | 2 条带,长度 2 |
| | | 1 条莫比乌斯带,长度 1 |
| 1 | 3 | 6 | 3 条带,长度 2 |
| 1 | 3 | 7 | 3 条带,长度 2 |
| | | 1 条莫比乌斯带,长度 1 |
| 2 | 1 | 2 | 2 条带,长度 1 |
| 2 | 2 | 3 | 3 条带,长度 1 |
| 2 | 3 | 4 | 4 条带,长度 1 |
一个环面可以被切割成具有偶数个半扭曲的莫比乌斯带,一个克莱因瓶可以沿着其长度方向对半切割以制成两条莫比乌斯带。此外,当解开时,两个彼此叠加的条带,每个条带都具有半扭曲,会形成一个具有四个扭曲的条带。
沿着边界将莫比乌斯带连接到圆盘的拓扑结果是一个实射影平面,它不能嵌入到  中。然而,有三个曲面是在
中。然而,有三个曲面是在  中实射影平面的表示,具有自相交,即博伊曲面、交叉帽和罗马曲面。
中实射影平面的表示,具有自相交,即博伊曲面、交叉帽和罗马曲面。
莫比乌斯带上的任何区域集合都可以仅使用六种颜色着色,如上面的Tietze 图所示。
另请参阅
博伊曲面,
交叉帽,
地图着色,
莫比乌斯带剖分,
不可定向曲面,
并合环,
棱柱环,
罗马曲面,
Tietze 图 在 课堂中探索此主题
使用 探索
参考文献
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 127-128, 1987.Bogomolny, A. "Möbius Strip." http://www.cut-the-knot.org/do_you_know/moebius.shtml.Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 243, 1976.Bool, F. H.; Kist, J. R.; Locher, J. L.; and Wierda, F. M. C. Escher: His Life and Complete Graphic Work. New York: Abrams, 1982.Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004. Dickau, R. "Spinning Möbius Strip Movie." http://mathforum.org/advanced/robertd/moebius.htmlDodson, C. T. J. and Parker, P. E. A User's Guide to Algebraic Topology. Dordrecht, Netherlands: Kluwer, pp. 121 and 284, 1997.Escher, M. C. "Moebius Strip I." Wood engraving and woodcut in red, green, gold and black, printed from 4 blocks. 1961. http://www.mcescher.com/Gallery/recogn-bmp/LW437.jpg.Escher, M. C. "Moebius Strip II (Red Ants)." Woodcut in red, black and grey-green, printed from 3 blocks. 1963. http://www.mcescher.com/Gallery/recogn-bmp/LW441.jpg.Forty, S. M.C. Escher. Cobham, England: TAJ Books, 2003.Gardner, M. "Möbius Bands." Ch. 9 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 123-136, 1978.Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 10, 1984.Geometry Center. "The Möbius Band." http://www.geom.umn.edu/zoo/features/mobius/.Gray, A. "The Möbius Strip." §14.3 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 325-326, 1997.Henle, M. A Combinatorial Introduction to Topology. New York: Dover, p. 110, 1994.Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 41-45, 1975.JavaView. "Classic Surfaces from Differential Geometry: Moebius Strip." http://www-sfb288.math.tu-berlin.de/vgp/javaview/demo/surface/common/PaSurface_MoebiusStrip.html.Kraitchik, M. §8.4.3 in Mathematical Recreations. New York: W. W. Norton, pp. 212-213, 1942.Listing and Tait. Vorstudien zur Topologie, Göttinger Studien, Pt. 10, 1847.Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 7, 1979.Möbius, A. F. Werke, Vol. 2. p. 519, 1858.Nordstrand, T. "Moebiusband." http://jalape.no/math/moebtxt.Pappas, T. "The Moebius Strip & the Klein Bottle," "A Twist to the Moebius Strip," "The 'Double' Moebius Strip." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 207, 1989.Pickover, C. A. The Möbius Strip: Dr. August Mobius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. New York: Thunder's Mouth Press, 2006.Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 269-274, 1999.Trott, M. "The Mathematica Guidebooks Additional Material: Rotating Möbius Bands." http://www.mathematicaguidebooks.org/additions.shtml#G_2_01.Underwood, M. "Mobius Scarf, Klein Bottle, Klein Bottle 'Hat'." http://www.woolworks.org/patterns/klein.txt.Wagon, S. "Rotating Circles to Produce a Torus or Möbius Strip." §7.4 in Mathematica in Action. New York: W. H. Freeman, pp. 229-232, 1991.
Dickau, R. "Spinning Möbius Strip Movie." http://mathforum.org/advanced/robertd/moebius.htmlDodson, C. T. J. and Parker, P. E. A User's Guide to Algebraic Topology. Dordrecht, Netherlands: Kluwer, pp. 121 and 284, 1997.Escher, M. C. "Moebius Strip I." Wood engraving and woodcut in red, green, gold and black, printed from 4 blocks. 1961. http://www.mcescher.com/Gallery/recogn-bmp/LW437.jpg.Escher, M. C. "Moebius Strip II (Red Ants)." Woodcut in red, black and grey-green, printed from 3 blocks. 1963. http://www.mcescher.com/Gallery/recogn-bmp/LW441.jpg.Forty, S. M.C. Escher. Cobham, England: TAJ Books, 2003.Gardner, M. "Möbius Bands." Ch. 9 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 123-136, 1978.Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 10, 1984.Geometry Center. "The Möbius Band." http://www.geom.umn.edu/zoo/features/mobius/.Gray, A. "The Möbius Strip." §14.3 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 325-326, 1997.Henle, M. A Combinatorial Introduction to Topology. New York: Dover, p. 110, 1994.Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 41-45, 1975.JavaView. "Classic Surfaces from Differential Geometry: Moebius Strip." http://www-sfb288.math.tu-berlin.de/vgp/javaview/demo/surface/common/PaSurface_MoebiusStrip.html.Kraitchik, M. §8.4.3 in Mathematical Recreations. New York: W. W. Norton, pp. 212-213, 1942.Listing and Tait. Vorstudien zur Topologie, Göttinger Studien, Pt. 10, 1847.Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 7, 1979.Möbius, A. F. Werke, Vol. 2. p. 519, 1858.Nordstrand, T. "Moebiusband." http://jalape.no/math/moebtxt.Pappas, T. "The Moebius Strip & the Klein Bottle," "A Twist to the Moebius Strip," "The 'Double' Moebius Strip." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 207, 1989.Pickover, C. A. The Möbius Strip: Dr. August Mobius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. New York: Thunder's Mouth Press, 2006.Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 269-274, 1999.Trott, M. "The Mathematica Guidebooks Additional Material: Rotating Möbius Bands." http://www.mathematicaguidebooks.org/additions.shtml#G_2_01.Underwood, M. "Mobius Scarf, Klein Bottle, Klein Bottle 'Hat'." http://www.woolworks.org/patterns/klein.txt.Wagon, S. "Rotating Circles to Produce a Torus or Möbius Strip." §7.4 in Mathematica in Action. New York: W. H. Freeman, pp. 229-232, 1991. Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 152-153 and 164, 1991.
Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 152-153 and 164, 1991.
请引用为
Weisstein, Eric W. "莫比乌斯带。" 来自 -- 资源。 https://mathworld.net.cn/MoebiusStrip.html
主题分类
(Dodson and Parker 1997, p. 125)。
的莫比乌斯带,其中圆心半径为
且高度为
可以参数化表示为
和
。在这种参数化中,莫比乌斯带因此是一个三次曲面,其方程为
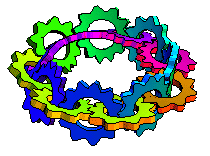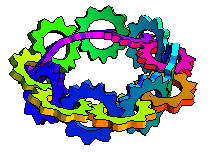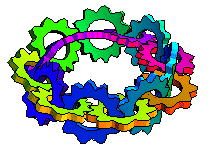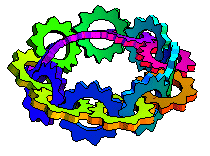
![R/(sqrt(4R^2+3s^2+2s[4Rcos(1/2t)+scost]))](/images/equations/MoebiusStrip/Inline30.svg)
![([2(R^2+s^2)+4Rscos(1/2t)+s^2cost]sin(1/2t))/(sqrt(4R^2+3s^2+2s[4Rcos(1/2t)+scost])),](/images/equations/MoebiusStrip/Inline33.svg)
![-(4R^2)/({4R^2+3s^2+2s[4Rcos(1/2t)+scost]}^2)](/images/equations/MoebiusStrip/Inline36.svg)
![(2[2(R^2+s^2)+4Rscos(1/2t)+s^2cost]sin(1/2t))/({4R^2+3s^2+2s[4Rcos(1/2t)+scost]}^2).](/images/equations/MoebiusStrip/Inline39.svg)
![ds=sqrt(x^('2)+y^('2))
=[1/(16)w^4cos^4(1/2t)+{[R+wcos(1/2t)]cost-1/2wsin(1/2t)sint}^4+{Rsint+1/4w[sin(1/2t)+3sin(3/2t)]}^4]^(1/2)](/images/equations/MoebiusStrip/NumberedEquation3.svg)
的积分,遗憾的是无法以闭合形式完成。请注意,虽然曲面在
处闭合,但这对应于底部边缘与顶部边缘连接,如上图所示,因此必须额外遍历
才能构成边界边缘的整个弧长。
中。然而,有三个曲面是在
中实射影平面的表示,具有自相交,即博伊曲面、交叉帽和罗马曲面。