主题
Search

罗马曲面

下载 Mathematica 笔记本下载 Wolfram 笔记本
RomanSurface

罗马曲面，也称为 Steiner 曲面（不要与 Steiner 曲面 类混淆，罗马曲面是 Steiner 曲面类的一个特例），是一种 四次 不可定向曲面。罗马曲面是通过将 莫比乌斯带缝合到 圆盘的边缘而获得的三种可能的曲面之一。另外两种是 Boy 曲面 和 交叉帽，所有这些都与 实射影平面 同胚 (Pinkall 1986)。

罗马曲面的中心点是一个普通的 三重点，具有 (+/-1,0,0)=(0,+/-1,0)=(0,0,+/-1)，并且三条自相交线的六个端点是奇异 夹点，也称为 夹点。罗马曲面本质上是由六个粘在一起的 交叉帽 组成，并包含双 无穷 个 圆锥曲线。

罗马曲面可以由以下方程给出

(x^2+y^2+z^2-k^2)^2=[(z-k)^2-2x^2][(z+k)^2-2y^2].
(1)

求解 z 得到方程组

z=(k(y^2-x^2)+/-(x^2-y^2)sqrt(k^2-x^2-y^2))/(2(x^2+y^2)).
(2)

如果曲面绕 z 轴 旋转 45 度，通过 旋转矩阵

R_z(45 degrees)=1/(sqrt(2))[1 1 0; -1 1 0; 0 0 1]
(3)

得到

[x^'; y^'; z^']=R_z(45 degrees)[x; y; z],
(4)

那么简单的方程

x^2y^2+x^2z^2+y^2z^2+2kxyz=0
(5)

结果。

罗马曲面也可以使用 不可定向曲面 的通用方法生成，使用多项式函数

f(x,y,z)=a(xy,yz,zx)
(6)

(Pinkall 1986)。设置

x=cosusinv
(7)
y=sinusinv
(8)
z=cosv
(9)

在前一个式子中得到

x(u,v)=1/2asin(2u)sin^2v
(10)
y(u,v)=1/2asinucos(2v)
(11)
z(u,v)=1/2acosusin(2v)
(12)

对于 u 在 [0,2pi) 中 和 v 在 [-pi/2,pi/2] 中。这给出了代数方程

x^2y^2+x^2z^2+y^2z^2-axyz=0,
(13)

对应于上述通用方程中的 a=-2k。 第一基本形式 和 第二基本形式 的系数稍微复杂，高斯曲率和平均曲率也是如此。所围成的 体积 由下式给出

V=1/6a^3,
(14)

其惯性矩张量为

I=[1/(10)Ma^2 0 0; 0 1/(10)Ma^2 0; 0 0 1/(10)Ma^2].
(15)
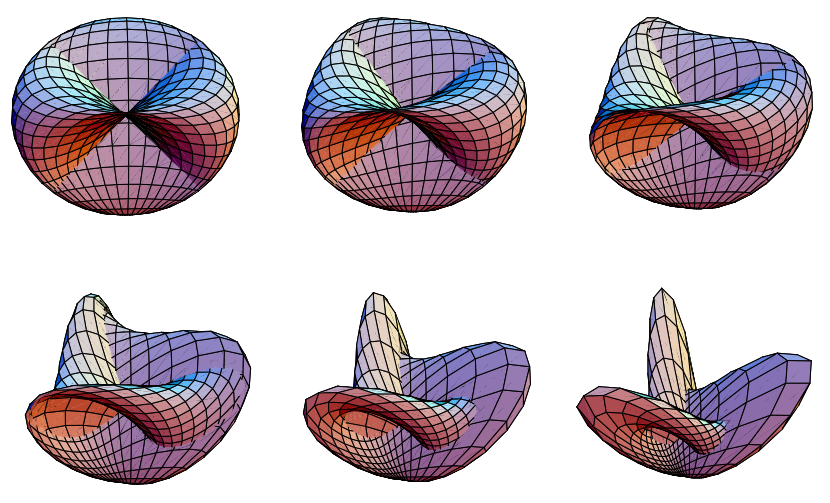
RomanBoy

罗马曲面和 Boy 曲面 之间的 同伦（平滑变形）由以下方程给出

x(u,v)=(sqrt(2)cos(2u)cos^2v+cosusin(2v))/(2-alphasqrt(2)sin(3u)sin(2v))
(16)
y(u,v)=(sqrt(2)sin(2u)cos^2v-sinusin(2v))/(2-alphasqrt(2)sin(3u)sin(2v))
(17)
z(u,v)=(3cos^2v)/(2-alphasqrt(2)sin(3u)sin(2v))
(18)

对于 u 在 [-pi/2,pi/2] 中 和 v 在 [0,pi] 中，当 alpha 从 0 变为 1 时。alpha=0 对应于罗马曲面，alpha=1 对应于 Boy 曲面。

参见

Boy 曲面, 交叉帽, 七面体, 莫比乌斯带, 不可定向曲面, 四次曲面, Steiner 曲面

使用 Wolfram|Alpha 探索

参考文献

Dharwadker, A. "Heptahedron and Roman Surface." Electronic Geometry Model No. 2003.05.001. http://www.eg-models.de/models/Surfaces/Algebraic_Surfaces/2003.05.001/.Fischer, G. (Ed.). Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Kommentarband. Braunschweig, Germany: Vieweg, p. 19, 1986.Fischer, G. (Ed.). Plates 42-44 and 108-114 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, pp. 42-44 and 108-109, 1986.Geometry Center. "The Roman Surface." http://www.geom.umn.edu/zoo/toptype/pplane/roman/.Gray, A. "Steiner's Roman Surface." Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 331-333, 1997.Nordstrand, T. "Steiner's Roman Surface." http://jalape.no/math/steintxt.Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, p. 64, 1986.更新链接Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/

请引用为

Weisstein, Eric W. "罗马曲面." 来自 MathWorld--Wolfram Web 资源. https://mathworld.net.cn/RomanSurface.html

主题分类