主题
Search

博伊曲面

下载 Mathematica 笔记本下载 Wolfram 笔记本

博伊曲面是一个不可定向曲面，它是通过将莫比乌斯带缝合到圆盘边缘而获得的曲面的一个可能的参数化表示。另外两个拓扑等价的参数化表示是交叉帽和罗马曲面。博伊曲面是无奇点的射影平面的模型，并且是一个六次曲面。

Boy surface sculpture at Oberwolfach

博伊曲面的雕塑，作为实射影平面在欧几里得三维空间中的特殊浸入，于 1991 年 1 月 28 日安装在奥伯沃尔法赫数学研究所图书馆大楼前 (奥伯沃尔法赫数学研究所；Karcher 和 Pinkall 1997)。

博伊曲面可以使用不可定向曲面的通用方法来描述，但这在 Apéry (1986) 找到解析方程之前是未知的。基于已被证明无法使用二次多项式描述曲面的事实，Hopf 曾推测四次多项式也不足以描述 (Pinkall 1986)。Apéry 的浸入证明了这个猜想是错误的，明确地给出了以不可定向曲面的标准形式表示的方程，

f_1(x,y,z)=1/2[(2x^2-y^2-z^2)(x^2+y^2+z^2)+2yz(y^2-z^2)+zx(x^2-z^2)+xy(y^2-x^2)]
(1)
f_2(x,y,z)=1/2sqrt(3)[(y^2-z^2)(x^2+y^2+z^2)+zx(z^2-x^2)+xy(y^2-x^2)]
(2)
f_3(x,y,z)=1/8(x+y+z)[(x+y+z)^3+4(y-x)(z-y)(x-z)].
(3)
BoySurface

代入

x=cosusinv
(4)
y=sinusinv
(5)
z=cosv
(6)

并令 u 在 [0,pi] 中 和 v 在 [0,pi] 中 即可得到博伊曲面，其三个视图如上所示。

的 R^3 参数化表示也可以写成

x=(sqrt(2)cos^2vcos(2u)+cosusin(2v))/(2-sqrt(2)sin(3u)sin(2v))
(7)
y=(sqrt(2)cos^2vsin(2u)-sinusin(2v))/(2-sqrt(2)sin(3u)sin(2v))
(8)
z=(3cos^2v)/(2-sqrt(2)sin(3u)sin(2v))
(9)

对于 u 在 [-pi/2,pi/2] 中 和 v 在 [0,pi] 中。

BoySurface2

使用此参数化表示获得的曲面的三个视图如上所示。

BoySurfaceBryant

R. Bryant 设计了漂亮的参数化表示

g_1=-3/2I[(z(1-z^4))/(z^6+sqrt(5)z^3-1)]
(10)
g_2=-3/2R[(z(1+z^4))/(z^6+sqrt(5)z^3-1)]
(11)
g_3=I[(1+z^6)/(z^6+sqrt(5)z^3-1)]-1/2,
(12)

其中

g=g_1^2+g_2^2+g_3^2
(13)

以及 |z|<=1，给出了曲面上点的笛卡尔坐标为

X=(g_1)/g
(14)
Y=(g_2)/g
(15)
Z=(g_3)/g.
(16)
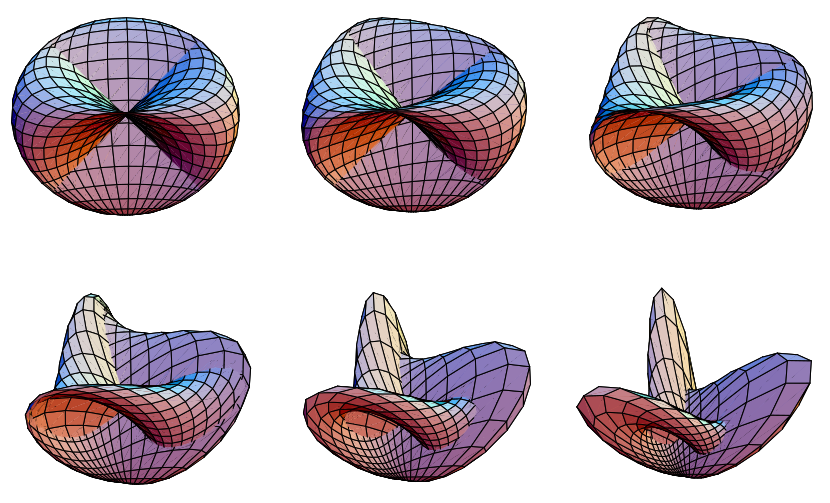
RomanBoy

实际上，罗马曲面和博伊曲面之间的同伦（光滑形变）由以下方程给出

x(u,v)=(sqrt(2)cos(2u)cos^2v+cosusin(2v))/(2-alphasqrt(2)sin(3u)sin(2v))
(17)
y(u,v)=(sqrt(2)sin(2u)cos^2v-sinusin(2v))/(2-alphasqrt(2)sin(3u)sin(2v))
(18)
z(u,v)=(3cos^2v)/(2-alphasqrt(2)sin(3u)sin(2v))
(19)

当 alpha 从 0 变到 1 时，其中 alpha=0 对应于罗马曲面，而 alpha=1 对应于如上所示的博伊曲面。

在 R^4 中，参数表示为

x_0=3[(u^2+v^2+w^2)(u^2+v^2)-sqrt(2)vw(3u^2-v^2)]
(20)
x_1=sqrt(2)(u^2+v^2)(u^2-v^2+sqrt(2)uw)
(21)
x_2=sqrt(2)(u^2+v^2)(2uv-sqrt(2)vw)
(22)
x_3=3(u^2+v^2)^2,
(23)

代数方程为

64(x_0-x_3)^3x_3^3-48(x_0-x_3)^2x_3^2(3x_1^2+3x_2^2+2x_3^2)+12(x_0-x_3)x_3[27(x_1^2+x_2^2)^2-24x_3^2(x_1^2+x_2^2)+36sqrt(2)x_2x_3(x_2^2-3x_1^2)+x_3^4]+(9x_1^2+9x_2^2-2x_3^2)[-81(x_1^2+x_2^2)^2-72x_3^2(x_1^2+x_2^2)+108sqrt(2)x_1x_3(x_1^2-3x_2^2)+4x_3^4]=0
(24)

(Apéry 1986)。令

x_0=1
(25)
x_1=x
(26)
x_2=y
(27)
x_3=z
(28)

给出了 R^3 中曲面的另一个版本。

另请参阅

交叉帽, 浸入, 莫比乌斯带, 不可定向曲面, 实射影平面, 罗马曲面, 六次曲面

使用 探索

参考文献

Apéry, F. "The Boy Surface." Adv. Math. 61, 185-266, 1986.Apéry, F. Models of the Real Projective Plane: Computer Graphics of Steiner and Boy Surfaces. Braunschweig, Germany: Vieweg, 1987.Apéry, F. "An Algebraic Halfway Model for the Eversion of the Sphere." Tôhoku Math. J. 44, 103-150, 1992.Apéry, F.; and Franzoni, G. "The Eversion of the Sphere: a Material Model of the Central Phase." Rendiconti Sem. Fac. Sc. Univ. Cagliari 69, 1-18, 1999.Boy, W. "Über die Curvatura integra und die Topologie geschlossener Flächen." Math. Ann 57, 151-184, 1903.Brehm, U. "How to Build Minimal Polyhedral Models of the Boy Surface." Math. Intell. 12, 51-56, 1990.Carter, J. S. "On Generalizing Boy Surface--Constructing a Generator of the 3rd Stable Stem." Trans. Amer. Math. Soc. 298, 103-122, 1986.Fischer, G. (编). Plates 115-120 收录于 Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, 页 110-115, 1986.Geometry Center. "Boy's Surface." http://www.geom.umn.edu/zoo/toptype/pplane/boy/.Hilbert, D. and Cohn-Vossen, S. §46-47 收录于 Geometry and the Imagination. New York: Chelsea, 1999.Karcher, H. and Pinkall, U. "Die Boysche Fläche in Oberwolfach." Mitteilungen der DMV, issue 1, 45-47, 1997.Mathematisches Forschungsinstitut Oberwolfach. "The Boy Surface at Oberwolfach." http://www.mfo.de/general/boy/.Nordstrand, T. "Boy's Surface." http://jalape.no/math/boytxt.Petit, J.-P. and Souriau, J. "Une représentation analytique de la surface de Boy." C. R. Acad. Sci. Paris Sér. 1 Math 293, 269-272, 1981.Pinkall, U. "Regular Homotopy Classes of Immersed Surfaces." Topology 24, 421-434, 1985.Pinkall, U. Mathematical Models from the Collections of Universities and Museums (编 G. Fischer). Braunschweig, Germany: Vieweg, 页 64-65, 1986.Stewart, I. Game, Set and Math. New York: Viking Penguin, 1991.Tardy, C. "La fameuse Surface de Boy." http://ctardy.free.fr/jadore/sciences/boy/.Toth, G. Finite Möbius Groups, Minimal Immersion of Spheres, and Moduli. Berlin: Springer-Verlag, 2002.Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 页 38-39, 2006. http://www.mathematicaguidebooks.org/.更新链接Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/

请引用本文为

Weisstein, Eric W. "博伊曲面。" 来自 Web 资源。 https://mathworld.net.cn/BoySurface.html

学科分类