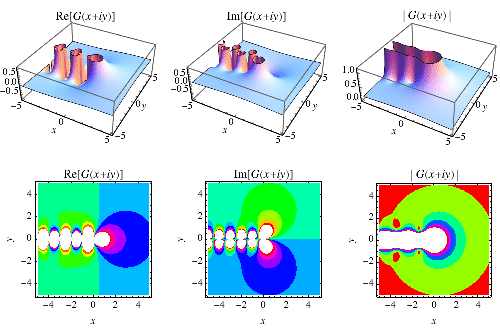
 |
正如 Erdelyi et al. (1981, p. 20) 所定义,-函数由下式给出
|
(1)
|
其中 是 双伽玛函数。积分表示由下式给出
|
(2)
| |||
|
(3)
|
对于 。
也由以下级数给出
|
(4)
|
并用 超几何函数 表示为
|
(5)
|
它服从以下函数关系
|
(6)
| |||
|
(7)
| |||
 |
(8)
|
 |
正如 Erdelyi et al. (1981, p. 20) 所定义,-函数由下式给出
|
(1)
|
其中 是 双伽玛函数。积分表示由下式给出
|
(2)
| |||
|
(3)
|
对于 。
也由以下级数给出
|
(4)
|
并用 超几何函数 表示为
|
(5)
|
它服从以下函数关系
|
(6)
| |||
|
(7)
| |||
 |
(8)
|
Weisstein, Eric W. "G-函数。" 来自 Web 资源。 https://mathworld.net.cn/G-Function.html