主题
Search

随机矩阵

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本

随机矩阵是给定类型和大小的矩阵，其条目由来自指定分布的随机数组成。

随机矩阵理论被引为凯瑟琳在 2005 年电影证明中证明素数定理中一个重要结果时使用的“现代工具”之一。

对于具有实n×n矩阵，其元素具有标准正态分布，实特征值的期望数量由下式给出

E_n=1/2+sqrt(2)(_2F_1(1,-1/2;n;1/2))/(B(n,1/2))
(1)
={sqrt(2)sum_(k=0)^(n/2-1)((4k-1)!!)/((4k)!!) for n even; 1+sqrt(2)sum_(k=1)^((n-1)/2)((4k-3)!!)/((4k-2)!!) for n odd,
(2)

其中 _2F_1(a,b;c;z) 是超几何函数，B(z,a) 是beta 函数（Edelman等， 1994；Edelman 和 Kostlan 1994）。E_n 具有渐近行为

E_n∼sqrt((2n)/pi).
(3)

令 p_(n,k) 为在n×n矩阵的复谱中恰好有 k 个实特征值的概率。Edelman (1997) 表明

p_(n,n)=2^(-n(n-1)/4),
(4)

这是所有 p_(n,k)s 中最小的概率。Kanzieper 和 Akemann (2005) 推导出了高斯实随机矩阵谱中预期实特征值数量的整个概率函数，如下所示

p_(n,k)=p_(n,n)F_l(p_1,...,p_l),
(5)

其中

F_l(p_1,...,p_l)=(-1)^lsum_(|lambda|=l)product_(j=1)^(g)1/(sigma_j!)(-(p_(l_j))/(l_j))^(sigma_j)
(6)
=1/(l!)Z_((1^l))(p_1,...,p_l).
(7)

在 (6) 中，求和运行在所有长度为 l 的划分 lambda 上，l 是复共轭特征值对的数量，Z_((1^l)) 是区域多项式。此外，(6) 使用了划分 lambda 的频率表示（Kanzieper 和 Akemann 2005）。参数 p_l 取决于 n（矩阵维度）的奇偶性，并由下式给出

p_j=Tr_((0,|_n/2_|-1))rho^^^j,
(8)

其中 Tr(A) 是矩阵迹，rho^^ 是一个 m×m 矩阵，其条目为

rho^^_(alpha,beta)^(even)=int_0^inftyy^(2(beta-alpha)-1)e^(y^2)erfc(ysqrt(2))×[(2alpha+1)L_(2alpha+1)^(2(beta-alpha)-1)(-2y^2)+2y^2L_(2alpha-1)^(2(beta-alpha)+1)(-2y^2)]dy
(9)
rho^^_(alpha,beta)^(odd)=rho^^_(alpha,beta)^(even)-(-4)^(m-beta)(m!)/((2m)!)((2beta)!)/(beta!)rho^^_(alpha,beta)^(even),
(10)

alpha 和 beta 在 0 和 m-1 之间变化，m=|_n/2_|，其中 |_x_| 是向下取整函数），L_j^alpha(z) 是广义拉盖尔多项式，erfc(z) 是互补误差函数 erfc (Kanzieper 和 Akemann 2005)。

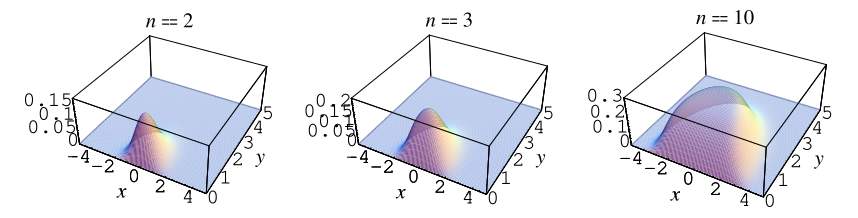
RandomMatrixComplexEigenvalues

Edelman (1997) 证明了实n×n矩阵的随机复共轭特征值对 x+/-iy 的密度，该矩阵的元素取自标准正态分布，为

rho_n(x,y)=sqrt(2/pi)ye^(y^2-x^2)erfc(sqrt(2)y)e_(n-2)(x^2+y^2)
(11)
=sqrt(2/pi)e^(2y^2)yerfc(sqrt(2)y)(Gamma(n-1,x^2+y^2))/(Gamma(n-1))
(12)

对于 y>=0，其中 erfc(z) 是 erfc（互补误差）函数，e_n(z) 是指数和函数，Gamma(a,x) 是上不完全伽马函数。在上半平面上积分（并乘以 2）得到复特征值的期望数量为

c_n=2int_(-infty)^inftyint_0^inftyrho_n(x,y)dydx
(13)
=n-1/2-sqrt(2)(_2F_1(1,-1/2;n;1/2))/(B(n,1/2))
(14)
=n-1/2-(2n-1)!!2^(-n)_2F^~_1(n-1,-1/2;n;-1)
(15)

（Edelman 1997）。前几个值为

c_1=0
(16)
c_2=2-sqrt(2)
(17)
c_3=2-1/2sqrt(2)
(18)
c_4=4-(11)/8sqrt(2)
(19)
c_5=4-(13)/(16)sqrt(2)
(20)

（OEIS A052928，A093605 和 A046161）。

吉尔科圆律考虑了一组随机n×n 实矩阵的特征值 lambda（可能是复数），这些矩阵的条目是独立的并取自标准正态分布，并指出当 n->infty 时，lambda/sqrt(n) 在复平面中的单位圆盘上均匀分布。

维格纳半圆律指出，对于大的 n×n 对称实矩阵，其元素取自分布，满足某些相当一般的性质，特征值的分布是半圆函数。

如果从以下矩阵中以 1/2 的概率选择 n 个矩阵 M_i 之一

M_+=[0 1; 1 1]
(21)
M_-=[0 1; 1 -1],
(22)

那么

lim_(n->infty)(ln||M_1...M_n||)/n=c,
(23)

其中 e^c=1.13198824... （OEIS A078416）和 ||M|| 表示矩阵谱范数（Bougerol 和 Lacroix 1985，第 11 页和 157 页；Viswanath 2000）。这与随机斐波那契数列中出现的常数相同。以下 Wolfram 语言 代码可用于估计此常数。

  With[{n = 100000},
    m = Fold[Dot, IdentityMatrix[2],
      {{0, 1}, {1, #}}& /@
        RandomChoice[{-1, 1}, {n}]
    ] // N;
    Log[Sqrt[Max[Eigenvalues[Transpose[m] . m]]]] /
    n
  ]

另请参阅

复矩阵，吉尔科圆律，整数矩阵，矩阵，随机斐波那契数列，实矩阵，维格纳半圆律

使用 Wolfram|Alpha 探索

参考文献

Bougerol, P. 和 Lacroix, J. 随机矩阵乘积及其在薛定谔算子中的应用。 巴塞尔，瑞士：Birkhäuser，1985 年。Chassaing, P.; Letac, G.; 和 Mora, M. “Brocot 序列和 SL_2(R) 上的随机游走。” 在群 VII 上的概率测度（H. Heyer 编辑）。纽约：Springer-Verlag，1984 年，第 36-48 页。Edelman, A. “随机实高斯矩阵具有 k 个实特征值的概率，相关分布和圆律。” J. Multivariate Anal. 60, 203-232, 1997.Edelman, A. 和 Kostlan, E. “随机多项式有多少个实零点？” Bull. Amer. Math. Soc. 32, 1-37, 1995.Edelman, A.; Kostlan, E.; 和 Shub, M. “随机矩阵有多少个实特征值？” J. Amer. Math. Soc. 7, 247-267, 1994.Furstenberg, H. “非交换随机乘积。” Trans. Amer. Math. Soc. 108, 377-428, 1963.Furstenberg, H. 和 Kesten, H. “随机矩阵的乘积。” Ann. Math. Stat. 31, 457-469, 1960.Girko, V. L. 随机行列式理论。 波士顿，MA：Kluwer，1990 年。Kanzieper, E. 和 Akemann, G. “Ginibre 随机实矩阵系综中实特征值的统计。” Phys. Rev. Lett. 95, 230201-1-230201-4, 2005.Katz, M. 和 Sarnak, P. 随机矩阵、弗罗贝尼乌斯特征值和单值性。 普罗维登斯，罗德岛州：Amer. Math. Soc., 1999.Lehmann, N. 和 Sommers, H.-J. “随机实矩阵的特征值统计。” Phys. Rev. Let. 67, 941-944, 1991.Mehta, M. L. 随机矩阵，第 3 版。 纽约：Academic Press，1991 年。Sloane, N. J. A. “整数序列在线百科全书”中的序列 A046161，A052928，A078416 和 A093605。Viswanath, D. “随机斐波那契数列和数字 1.13198824....” Math. Comput. 69, 1131-1155, 2000.

在 Wolfram|Alpha 上引用

随机矩阵

请引用为

Weisstein, Eric W. “随机矩阵”。来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/RandomMatrix.html

主题分类