主题
Search

椭圆 Lambda 函数

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
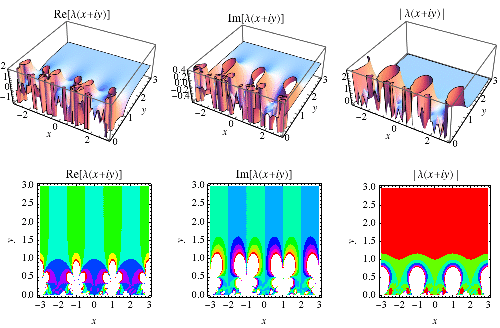
EllipticLambdaReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

椭圆 lambda 函数 lambda(tau) 是一个 lambda-模函数，定义在上半平面上，由下式给出

lambda(tau)=(theta_2^4(0,q))/(theta_3^4(0,q)),
(1)

其中 tau 是半周期比，q 是nome

q=e^(ipitau)
(2)

且 theta_i(z,q) 是 雅可比 theta 函数。

椭圆 lambda 函数本质上与逆 nome 相同，区别在于椭圆 lambda 函数是半周期比 tau 的函数，而逆 nome 是 nome q 的函数，其中 q 本身是 tau 的函数。

它在 Wolfram Language 函数中实现ModularLambda[tau]。

椭圆 lambda 函数 lambda(tau) 满足以下函数方程

lambda(tau+2)=lambda(tau)
(3)
lambda(tau/(2tau+1))=lambda(tau).
(4)

lambda(tau) 具有级数展开

lambda(tau)=16q-128q^2+704q^3-3072q^4+11488q^5+...
(5)

(OEIS A115977)，且 16/lambda(tau) 具有级数展开

(16)/(lambda(tau))=1/q+8+20q-62q^3+216q^5-641q^7+...
(6)

(OEIS A029845; Conway and Norton 1979; Borwein and Borwein 1987, p. 117)。

lambda^*(r) 给出了椭圆模量 k_r 的值，对于该值，互补K^'(k)=K(sqrt(1-k^2)) 和标准第一类完全椭圆积分 K(k) 通过下式相关

(K^'(k_r))/(K(k_r))=sqrt(r),
(7)

即，椭圆积分奇异值 对于 r。它可以从下式计算得出

lambda^*(r)=k(q_r)=(theta_2^2(0,q_r))/(theta_3^2(0,q_r)),
(8)

其中

q_r=e^(-pisqrt(r))
(9)

且 theta_i 是一个 雅可比 theta 函数。lambda(tau) 与 lambda^*(r) 通过下式相关

lambda^*(r)=sqrt(lambda(isqrt(r))).
(10)

对于所有有理数 r，K(lambda^*(r)) 和 E(lambda^*(r)) 被称为椭圆积分奇异值，并且可以用有限数量的伽玛函数表示 (Selberg and Chowla 1967)。lambda^*(r) 对于小 r 的值包括

lambda^*(1)=1/2sqrt(2)
(11)
lambda^*(2)=sqrt(2)-1
(12)
lambda^*(3)=1/4sqrt(2)(sqrt(3)-1)
(13)
lambda^*(4)=3-2sqrt(2)
(14)
lambda^*(5)=sqrt(1/2-sqrt(sqrt(5)-2))
(15)
lambda^*(6)=(2-sqrt(3))(sqrt(3)-sqrt(2))
(16)
lambda^*(7)=1/8sqrt(2)(3-sqrt(7))
(17)
lambda^*(8)=(sqrt(2)+1-sqrt(2sqrt(2)+2))^2
(18)
lambda^*(9)=1/2(sqrt(2)-3^(1/4))(sqrt(3)-1)
(19)
lambda^*(10)=(sqrt(10)-3)(sqrt(2)-1)^2
(20)
lambda^*(11)=1/(12)sqrt(6)(sqrt(1+2x_(11)-4x_(11)^(-1))-sqrt(11+2x_(11)-4x_(11)^(-1)))
(21)
lambda^*(12)=(sqrt(3)-sqrt(2))^2(sqrt(2)-1)^2
(22)
lambda^*(13)=1/2(sqrt(5sqrt(13)-17)-sqrt(19-5sqrt(13)))
(23)
lambda^*(14)=-11-8sqrt(2)-2(sqrt(2)+2)sqrt(5+4sqrt(2))+sqrt(11+8sqrt(2))(2+2sqrt(2)+sqrt(2)sqrt(5+4sqrt(2)))
(24)
lambda^*(15)=1/(16)sqrt(2)(3-sqrt(5))(sqrt(5)-sqrt(3))(2-sqrt(3))
(25)
lambda^*(16)=33+24sqrt(2)-4sqrt(140+99sqrt(2))
(26)
lambda^*(18)=(sqrt(2)-1)^3(2-sqrt(3))^2,
(27)

其中

x_(11)=(17+3sqrt(33))^(1/3).
(28)

这些值的代数阶数由 2, 2, 4, 2, 8, 4, 4, 4, 8, 4, 12, 4, 8, 8, 8, 4, ... 给出 (OEIS A084540)。

一些额外的精确值由下式给出

lambda^*(22)=(3sqrt(11)-7sqrt(2))(10-3sqrt(11))
(29)
lambda^*(30)=(sqrt(3)-sqrt(2))^2(2-sqrt(3))(sqrt(6)-sqrt(5))(4-sqrt(15))
(30)
lambda^*(34)=(sqrt(2)-1)^2(3sqrt(2)-sqrt(17))×(sqrt(297+72sqrt(17))-sqrt(296+72sqrt(17)))
(31)
lambda^*(42)=(sqrt(2)-1)^2(2-sqrt(3))^2(sqrt(7)-sqrt(6))(8-3sqrt(7))
(32)
lambda^*(58)=(13sqrt(58)-99)(sqrt(2)-1)^6
(33)
lambda^*(210)=(sqrt(2)-1)^2(2-sqrt(3))(sqrt(7)-sqrt(6))^2(8-3sqrt(7))×(sqrt(10)-3)^2(4-sqrt(15))^2(sqrt(15)-sqrt(14))(6-sqrt(35)).
(34)

对于有理数 r 也可以找到精确值，包括

lambda^*(1/2)=sqrt(2(sqrt(2)-1))
(35)
lambda^*(1/3)=1/2sqrt(2+sqrt(3))
(36)
lambda^*(2/3)=(2-sqrt(3))(sqrt(2)+sqrt(3))
(37)
lambda^*(1/4)=2sqrt(3sqrt(2)-4)
(38)
lambda^*(3/4)=(x^8+3328x^6+768x^4-8192x^2+4096)_3
(39)
lambda^*(1/5)=sqrt(1/2+sqrt(sqrt(5)-2))
(40)
lambda^*(2/5)=(sqrt(10)-3)(sqrt(2)+1)^2
(41)
lambda^*(3/5)=1/4sqrt(8+sqrt(3/2(23-7sqrt(5))))
(42)
lambda^*(4/5)=(x^8-280x^7-292x^6-680x^5+2758x^4-680x^3-292x^2-280x+1)_2
(43)
lambda^*(2/(29))=(13sqrt(58)-99)(sqrt(2)+1)^6,
(44)

其中 (P(x))_n 是一个 多项式根。

lambda^*(r) 与 拉马努金 g- 和 G-函数 相关

lambda^*(n)=1/2(sqrt(1+G_n^(-12))-sqrt(1-G_n^(-12)))
(45)
lambda^*(n)=g_n^6(sqrt(g_n^(12)+g_n^(-12))-g_n^6).
(46)

另请参阅

戴德金 Eta 函数, 椭圆 Alpha 函数, 第一类椭圆积分, 椭圆模量, 椭圆积分奇异值, 逆 Nome, j-函数, 雅可比 Theta 函数, 克莱因绝对不变量, 模函数, 模群 Lambda, 拉马努金 g- 和 G-函数, 韦伯函数

相关 Wolfram 站点

http://functions.wolfram.com/EllipticFunctions/ModularLambda/

使用 Wolfram|Alpha 探索

参考文献

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 139 and 298, 1987.Bowman, F. Introduction to Elliptic Functions, with Applications. New York: Dover, pp. 75, 95, and 98, 1961.Conway, J. H. and Norton, S. P. "Monstrous Moonshine." Bull. London Math. Soc. 11, 308-339, 1979.Selberg, A. and Chowla, S. "On Epstein's Zeta-Function." J. reine angew. Math. 227, 86-110, 1967.Sloane, N. J. A. Sequences A029845, A084540, and A115977 in "The On-Line Encyclopedia of Integer Sequences."Watson, G. N. "Some Singular Moduli (1)." Quart. J. Math. 3, 81-98, 1932.

在 Wolfram|Alpha 上被引用

椭圆 Lambda 函数

请引用为

Weisstein, Eric W. "椭圆 Lambda 函数。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/EllipticLambdaFunction.html

主题分类