设椭圆模量  满足
满足  , 并且 雅可比振幅 由
, 并且 雅可比振幅 由  给出,其中
给出,其中  。则第一类不完全椭圆积分定义为
。则第一类不完全椭圆积分定义为
 |
(1)
|
第一类椭圆积分在 Wolfram 语言 中实现为EllipticF[phi, m] (注意使用参数  而不是模数
而不是模数  )。
)。
设
方程 (1) 可以写成
设
则该积分也可以写成
 |
(9)
|
其中  是互补椭圆模量。
是互补椭圆模量。
 的反函数由雅可比振幅给出
的反函数由雅可比振幅给出
 |
(10)
|
积分
 |
(11)
|
它出现在计算单摆周期中,也是第一类椭圆积分。使用
写成
所以
 |
(17)
|
现在设
 |
(18)
|
因此,当  从 0 变化到
从 0 变化到  时,角度
时,角度  转换为
转换为
![phi=sin^(-1)[(sin(1/2theta))/(sin(1/2theta_0))],](/images/equations/EllipticIntegraloftheFirstKind/NumberedEquation7.svg) |
(19)
|
其范围从 0 到  。取微分得到
。取微分得到
 |
(20)
|
或
 |
(21)
|
代入得到
所以
进行略有不同的替换  ,因此
,因此  导致一个等价的,但更复杂的表达式,涉及第一类不完全椭圆积分,
导致一个等价的,但更复杂的表达式,涉及第一类不完全椭圆积分,
因此,恒等式
 |
(29)
|
至少在复平面的某些区域上成立。适用区域为 ![-pi/2<R[z]<pi/2](/images/equations/EllipticIntegraloftheFirstKind/Inline72.svg) ,如上所示。
,如上所示。
第一类椭圆积分满足
 |
(30)
|
 的特殊值包括
的特殊值包括
其中  被称为第一类完全椭圆积分。
被称为第一类完全椭圆积分。
另请参阅
第一类完全椭圆积分,
椭圆特征,
第二类椭圆积分,
第三类椭圆积分,
椭圆积分奇值,
椭圆模量,
高斯变换,
雅可比振幅,
兰登变换,
勒让德关系,
模角,
参数
相关的 Wolfram 站点
http://functions.wolfram.com/EllipticIntegrals/EllipticF/
使用 探索
参考文献
Abramowitz, M. and Stegun, I. A. (Eds.). "Elliptic Integrals." Ch. 17 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 587-607, 1972.Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.Spanier, J. and Oldham, K. B. "The Complete Elliptic Integrals  and
and  " and "The Incomplete Elliptic Integrals
" and "The Incomplete Elliptic Integrals  and
and  ." Chs. 61-62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.Tölke, F. "Parameterfunktionen." Ch. 3 in Praktische Funktionenlehre, zweiter Band: Theta-Funktionen und spezielle Weierstraßsche Funktionen. Berlin: Springer-Verlag, pp. 83-115, 1966.Tölke, F. "Umkehrfunktionen der Jacobischen elliptischen Funktionen und elliptische Normalintegrale erster Gattung. Elliptische Amplitudenfunktionen sowie Legendresche F- und E-Funktion. Elliptische Normalintegrale zweiter Gattung. Jacobische Zeta- und Heumansche Lambda-Funktionen," and "Normalintegrale dritter Gattung. Legendresche
." Chs. 61-62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.Tölke, F. "Parameterfunktionen." Ch. 3 in Praktische Funktionenlehre, zweiter Band: Theta-Funktionen und spezielle Weierstraßsche Funktionen. Berlin: Springer-Verlag, pp. 83-115, 1966.Tölke, F. "Umkehrfunktionen der Jacobischen elliptischen Funktionen und elliptische Normalintegrale erster Gattung. Elliptische Amplitudenfunktionen sowie Legendresche F- und E-Funktion. Elliptische Normalintegrale zweiter Gattung. Jacobische Zeta- und Heumansche Lambda-Funktionen," and "Normalintegrale dritter Gattung. Legendresche  -Funktion. Zurückführung des allgemeinen elliptischen Integrals auf Normalintegrale erster, zweiter, und dritter Gattung." Chs. 6-7 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 58-144, 1967.Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.
-Funktion. Zurückführung des allgemeinen elliptischen Integrals auf Normalintegrale erster, zweiter, und dritter Gattung." Chs. 6-7 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 58-144, 1967.Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.在 中被引用
第一类椭圆积分
请引用为
Weisstein, Eric W. "第一类椭圆积分。" 来自 Web 资源。 https://mathworld.net.cn/EllipticIntegraloftheFirstKind.html
主题分类
满足
, 并且 雅可比振幅 由
给出,其中
。则第一类不完全椭圆积分定义为
而不是模数
)。


是互补椭圆模量。
的反函数由雅可比振幅给出



从 0 变化到
时,角度
转换为
![phi=sin^(-1)[(sin(1/2theta))/(sin(1/2theta_0))],](/images/equations/EllipticIntegraloftheFirstKind/NumberedEquation7.svg)
。取微分得到


,因此
导致一个等价的,但更复杂的表达式,涉及第一类不完全椭圆积分,

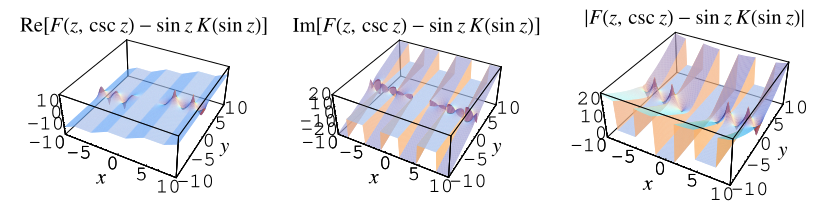
,如上所示。
的特殊值包括
被称为第一类完全椭圆积分。