规则 102 是 Stephen Wolfram 在 1983 年引入的 elementary cellular automaton 规则之一 (Wolfram 1983, 2002)。它根据单元格的颜色及其直接邻居指定单元格中的下一个颜色。其规则结果编码在二进制表示 中。上面说明了此规则以及它在 15 步后产生的单个黑色单元格的演变过程 (OEIS A075439; Wolfram 2002, p. 55)。
从单个黑色单元格开始,连续世代通过解释二进制数 1, 6, 20, 120, 272, 1632, 5440, 32640, ... (OEIS A117998) 给出。省略尾随零(三角形的第 步中的右侧
个单元格始终为 0)得到 1, 3, 5, 15, 17, 51, 85, 255, 257, 771, ... (OEIS A001317),这些数字只是前一个数字除以
,并且其二进制表示形式为 1, 11; 101, 1111, 10001, ... (OEIS A047999)。令人惊讶的是,这正是 Sierpiński sieve。
镜像图像是 规则 60,补码是规则 153,镜像补码是规则 195。
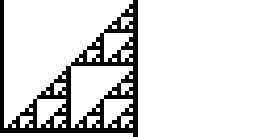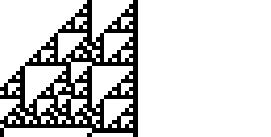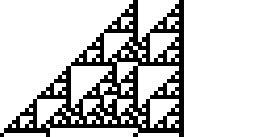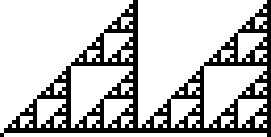
规则 102 是八个 additive elementary cellular automata 之一 (Wolfram 2002, p. 953)。