加法元胞自动机是一种元胞自动机,其规则与状态的加法兼容。通常,这种加法来源于模运算。加法规则允许独立计算不同初始条件的演化,然后通过简单相加来组合结果。因此,可以通过将单个细胞的演化与适当的卷积核(在双色自动机的情况下,这将对应于初始“活动”细胞的集合)进行卷积,非常有效地计算任意起始条件的结果。
一个加法元胞自动机的简单例子是由规则 90 基本元胞自动机提供的。从该规则的图形表示可以看出,作为左邻居、中心邻居和右邻居的函数,该规则仅仅由左邻居和右邻居的规则之和模 2 给出,其中白色细胞被赋值为 0,黑色细胞被赋值为 1。(这等同于 异或 运算,意味着“相加”两个白色细胞或两个黑色细胞得到一个白色细胞,而相加一个白色细胞和一个黑色细胞得到一个黑色细胞。)例如,规则 (1, 1, 1) 是 ,规则 (1, 1, 0) 是
,规则 (1, 0, 1) 是
,等等。对
种可能的邻居状态中的每一种重复此操作,得到
|
(1)
|
这正是定义规则 90 的二进制字符串(此规则被分配数字 90 是因为 在二进制中)。

规则 90 的移位版本的演化如上图所示。左图显示了规则 90 对由单个黑色方块组成的初始条件进行的 31 次迭代。向右移动,每个图都显示了在起始条件中添加一个位移为 的额外黑色单元格的结果,每帧增加一代。

上面的图示更明确地显示了可加性。在这个动画中,每一帧对应于初始条件,其中右侧单元格进一步向右移动一个单位。可以看出,不重叠的模式部分保持不变,而重叠部分在异或运算下是可加的。
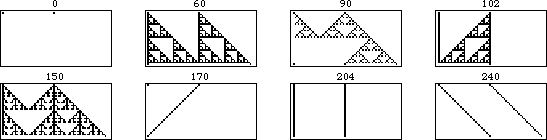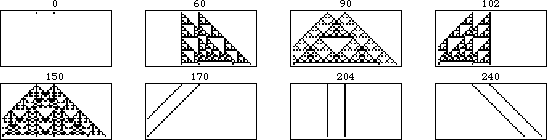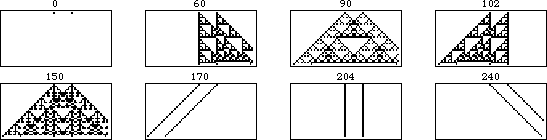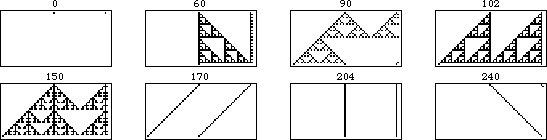
一般来说,具有 种颜色的元胞自动机是加法的,如果其规则可以写成其邻居的整数倍之和(模
),其中整数的范围可以从 0 到
。因此,在
种可能的规则中,有
种加法规则,具有
种颜色和范围
(Wolfram 2002, p. 952)。下表总结了基本元胞自动机的八个加法规则(
和
给出
)。在表中,
表示位于相对于中心位置
的邻居。
对于上述自动机的可加性,所需的性质是结合律和交换律。可以将可加性的概念推广到其他类型的加法。一般来说,设 表示
的元胞自动机演化历史,设
表示作用于细胞值的二元运算符,并通过扩展作用于它们的状态和演化。那么,
是关于
的加法元胞自动机,如果
|
(2)
|
一些元胞自动机没有有趣的 ,但另一些则有,并且这些加法可以用来加速计算。
规则 250 提供了在 或运算()下的加法基本元胞自动机的另一个例子。通过检查规则集,可以验证在每种情况下,如果任一(或两者)邻居是黑色的,则结果状态为黑色,并且仅当两个邻居都是白色时才为白色。这对应于规则集
|
(3)
|
这与规则 250 的定义相同。


上面说明了前几个移位的逐代差异以及作为移位函数的整个模式。
由于可加性,加法元胞自动机的演化行为类似于线性偏微分方程的解。特别是,它们允许格林函数的类似物,这样,给定一个初始条件,可以通过将单个细胞的演化(可以看作是积分核的类似物)与初始条件进行卷积来找到结果演化(Wolfram 2002, p. 952)。