主题
Search

Erf

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
Erf

erf(z) 是在积分正态分布（它是高斯函数的归一化形式）中遇到的“误差函数”。它是由以下定义的整函数

erf(z)=2/(sqrt(pi))int_0^ze^(-t^2)dt.
(1)

请注意，一些作者（例如，Whittaker 和 Watson 1990，第 341 页）将 erf(z) 定义为没有前导因子 2/sqrt(pi)。

Erf 在 Wolfram 语言 中实现为Erf[z]。 给出 erf(z_1)-erf(z_0) 的双参数形式也实现为Erf[z0, z1]。

Erf 满足以下恒等式

erf(z)=1-erfc(z)
(2)
=(2z)/(sqrt(pi))_1F_1(1/2;3/2;-z^2)
(3)
=(2ze^(-z^2))/(sqrt(pi))_1F_1(1;3/2;z^2),
(4)

其中 erfc(z) 是 erfc，互补误差函数，而 _1F_1(a;b;z) 是第一类合流超几何函数。对于 z>0，

erf(z)=pi^(-1/2)gamma(1/2,z^2),
(5)

其中 gamma(a,x) 是不完全伽玛函数。

Erf 也可以定义为麦克劳林级数

erf(z)=2/(sqrt(pi))sum_(n=0)^(infty)((-1)^nz^(2n+1))/(n!(2n+1))
(6)
=2/(sqrt(pi))(z-1/3z^3+1/(10)z^5-1/(42)z^7+1/(216)z^9+...)
(7)

(OEIS A007680)。 同样地，

erf^2(z)=4/pi(z^2-2/3z^4+(14)/(45)z^6-4/(35)z^8+(166)/(4725)z^(10)+...)
(8)

(OEIS A103979 和 A103980)。

对于 x<<1，erf(x) 可以从以下公式计算

erf(x)=1/(sqrt(pi))e^(-x^2)sum_(n=0)^(infty)((2x)^(2n+1))/((2n+1)!!)
(9)
=2/(sqrt(pi))e^(-x^2)[x+(2x^3)/(1·3)+(4x^5)/(1·3·5)+...]
(10)

(OEIS A000079 和 A001147；Acton 1990)。

对于 x>>1，

erf(x)=2/(sqrt(pi))(int_0^inftye^(-t^2)dt-int_x^inftye^(-t^2)dt)
(11)
=1-2/(sqrt(pi))int_x^inftye^(-t^2)dt.
(12)

使用分部积分得到

int_x^inftye^(-t^2)dt=-1/2int_x^infty1/td(e^(-t^2))
(13)
=-1/2[(e^(-t^2))/t]_x^infty-1/2int_x^infty(e^(-t^2)dt)/(t^2)
(14)
=(e^(-x^2))/(2x)+1/4int_x^infty1/(t^3)d(e^(-t^2))
(15)
=(e^(-x^2))/(2x)-(e^(-x^2))/(4x^3)-...,
(16)

因此

erf(x)=1-(e^(-x^2))/(sqrt(pi)x)(1-1/(2x^2)-...)
(17)

继续此过程得到渐近级数

erf(x)∼1-(e^(-x^2))/(sqrt(pi))sum_(n=0)^(infty)((-1)^n(2n-1)!!)/(2^n)x^(-(2n+1))
(18)
∼1-(e^(-x^2))/(sqrt(pi))(x^(-1)-1/2x^(-3)+3/4x^(-5)-(15)/8x^(-7)
(19)
+(105)/(16)x^(-9)+...)
(20)

(OEIS A001147 和 A000079)。

Erf 的值如下

erf(0)=0
(21)
erf(infty)=1.
(22)

它是奇函数

erf(-z)=-erf(z),
(23)

并满足

erf(z)+erfc(z)=1.
(24)

Erf 可以用第一类合流超几何函数 M 表示为

erf(z)=(2z)/(sqrt(pi))M(1/2,3/2,-z^2)
(25)
=(2z)/(sqrt(pi))e^(-z^2)M(1,3/2,z^2).
(26)

它的导数是

(d^n)/(dz^n)erf(z)=(-1)^(n-1)2/(sqrt(pi))H_(n-1)(z)e^(-z^2),
(27)

其中 H_n 是埃尔米特多项式。一阶导数是

d/(dz)erf(z)=2/(sqrt(pi))e^(-z^2),
(28)

积分是

interf(z)dz=zerf(z)+(e^(-z^2))/(sqrt(pi)).
(29)
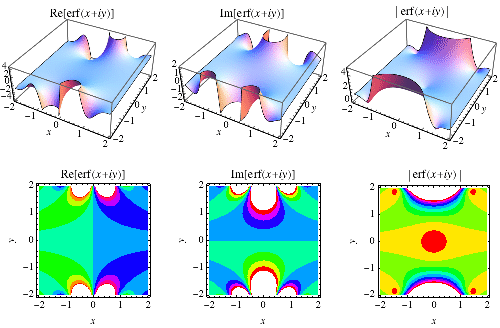ErfReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

Erf 也可以扩展到复平面，如上图所示。

一个简单的涉及 erf 的积分，Wolfram 语言 无法计算，由下式给出

int_0^pe^(-x^2)erf(p-x)dx=1/2sqrt(pi)[erf(1/2sqrt(2)p)]^2
(30)

(M. R. D'Orsogna，私人通讯，2004 年 5 月 9 日)。更复杂的积分包括

int_0^infty(e^(-(p+x)y))/(pi(p+x))sin(asqrt(x))dx=-sinh(asqrt(p)) +(e^(-asqrt(p)))/2erf(a/(2sqrt(y))-sqrt(py))+(e^(asqrt(p)))/2erf(a/(2sqrt(y))+sqrt(py)) int_0^infty(sqrt(x)e^(-(p+x)y))/(pi(p+x))cos(asqrt(x))dx=(e^(-[py+a^2/(4y)]))/(sqrt(piy))+sqrt(p)[-cosh(asqrt(p))-(e^(-asqrt(p)))/2erf(a/(2sqrt(y))-sqrt(py))+(e^(asqrt(p)))/2erf(a/(2sqrt(y))+sqrt(py))]
(31)

(M. R. D'Orsogna，私人通讯，2005 年 12 月 15 日)。

Erf 有连分数

int_0^xe^(-t^2)dt=1/2sqrt(pi)erf(x)
(32)
=1/2sqrt(pi)-(1/2e^(-x^2))/(x+1/(2x+2/(x+3/(2x+4/(x+...)))))
(33)

(Wall 1948，第 357 页)，最早由拉普拉斯于 1805 年和勒让德于 1826 年提出 (Olds 1963，第 139 页)，由雅可比证明，并由拉马努金重新发现 (Watson 1928；Hardy 1999，第 8-9 页)。

涉及 erf(x) 的定积分包括 涉及 erf(x) 的定积分包括

int_0^inftye^(-px^2)erf(ax)erf(bx)dx=1/(sqrt(pip))tan^(-1)((ab)/(sqrt(p(a^2+b^2+p))))
(34)
int_0^inftyxe^(-px^2)erf(ax)erf(bx)erf(cx)dx=1/(pip)[a/(sqrt(a^2+p))tan^(-1)((bc)/(sqrt((a^2+b^2+c^2+p)(a^2+p))))+b/(sqrt(b^2+p))tan^(-1)((ac)/(sqrt((a^2+b^2+c^2+p)(b^2+p))))+c/(sqrt(c^2+p))tan^(-1)((ab)/(sqrt((a^2+b^2+c^2+p)(c^2+p))))]
(35)
int_0^inftye^(-x)erf(sqrt(x))dx=1/2sqrt(2)
(36)
int_0^inftye^(-x)erf^2(sqrt(x))dx=(2sqrt(2)cot^(-1)(sqrt(2)))/pi
(37)
int_0^inftye^(-x)erf^3(sqrt(x))dx=(3sqrt(2)cot^(-1)(2sqrt(2)))/pi.
(38)

其中前两个出现在 Prudnikov et al. （1990，第 123 页，方程式 2.8.19.8 和 2.8.19.11）中，其中 R[p]>0，|arg(a)|,|argb|,|argc|<pi/4。

复数对 erf(x) 的推广定义为

w(z)=e^(-z^2)erfc(-iz)
(39)
=e^(-z^2)(1+(2i)/(sqrt(pi))int_0^ze^(t^2)dt).
(40)

仅在上半平面 I[z]>0 中有效的积分表示由下式给出

w(z)=i/piint_(-infty)^infty(e^(-t^2))/(z-t)dt
(41)
=(2iz)/piint_0^infty(e^(-t^2))/(z^2-t^2)dt.
(42)

另请参阅

道森积分, Erfc, Erfi, 菲涅尔积分, 高斯函数, 高斯积分, 反误差函数, 正态分布函数, 欧文 T 函数, 概率积分 在 MathWorld 课堂中探索此主题

相关的 Wolfram 网站

http://functions.wolfram.com/GammaBetaErf/Erf/, http://functions.wolfram.com/GammaBetaErf/Erf2/

使用 Wolfram|Alpha 探索

参考文献

Abramowitz, M. and Stegun, I. A. (Eds.). "误差函数和菲涅尔积分。" 第 7 章，数学函数手册，包含公式、图表和数学表格，第 9 次印刷。 New York: Dover, pp. 297-309, 1972.Acton, F. S. 有效的数值方法，第 2 次印刷。 Washington, DC: Math. Assoc. Amer., p. 16, 1990.Arfken, G. 物理学家的数学方法，第 3 版。 Orlando, FL: Academic Press, pp. 568-569, 1985.Hardy, G. H. 拉马努金：关于他的生活和工作提出的主题的十二次讲座，第 3 版。 New York: Chelsea, 1999.Havil, J. 伽玛：探索欧拉常数。 Princeton, NJ: Princeton University Press, p. 105, 2003.Olds, C. D. 连分数。 New York: Random House, 1963.Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. 积分与级数，第 2 卷：特殊函数。 New York: Gordon and Breach, 1990.Sloane, N. J. A. Sequences A000079/M1129, A001147/M3002, A007680/M2861, A103979, A103980 in "整数序列在线百科全书."Spanier, J. and Oldham, K. B. "误差函数 erf(x) 及其补函数 erfc(x)。" 第 40 章，函数图集。 Washington, DC: Hemisphere, pp. 385-393, 1987.Wall, H. S. 连分数解析理论。 New York: Chelsea, 1948.Watson, G. N. "拉马努金提出的定理（四）：关于近似积分和级数求和的定理。" J. London Math. Soc. 3, 282-289, 1928.Whittaker, E. T. and Robinson, G. "误差函数。" §92 in 观测演算：数值数学专著，第 4 版。 New York: Dover, pp. 179-182, 1967.Whittaker, E. T. and Watson, G. N. 现代分析教程，第 4 版。 Cambridge, England: Cambridge University Press, 1990.

在 Wolfram|Alpha 中被引用

Erf

引用为

Weisstein, Eric W. "Erf." 来自 MathWorld--Wolfram 网络资源。 https://mathworld.net.cn/Erf.html

主题分类