艾里函数共有四种变体:  ,
,  ,
,  , 和
, 和  。 其中,
。 其中,  和
和  是最常见的,而
是最常见的,而  和
和  则较少见。艾里函数常出现在物理学中,尤其是在光学、量子力学、电磁学和辐射传输中。
则较少见。艾里函数常出现在物理学中,尤其是在光学、量子力学、电磁学和辐射传输中。
 和
和  是 整函数。
是 整函数。
哈代构建了艾里函数的一种推广。
艾里函数  和
和  函数在上面沿实轴绘制。
函数在上面沿实轴绘制。
 和
和  函数被定义为以下方程的两个线性独立解
函数被定义为以下方程的两个线性独立解
 |
(1)
|
(Abramowitz 和 Stegun 1972, pp. 446-447; 如上图所示),写成以下形式
 |
(2)
|
其中
其中  是一个合流超几何极限函数。这些函数在 Wolfram 语言中实现为AiryAi[z] 和AiryBi[z]。它们的导数实现为AiryAiPrime[z] 和AiryBiPrime[z]。
是一个合流超几何极限函数。这些函数在 Wolfram 语言中实现为AiryAi[z] 和AiryBi[z]。它们的导数实现为AiryAiPrime[z] 和AiryBiPrime[z]。
对于特殊情况  , 这些函数可以写成
, 这些函数可以写成
其中  是一个第一类修正贝塞尔函数,而
是一个第一类修正贝塞尔函数,而  是一个第二类修正贝塞尔函数。
是一个第二类修正贝塞尔函数。
 在复平面中的图示如上所示。
在复平面中的图示如上所示。
类似地,  的图示也显示在上面。
的图示也显示在上面。
艾里  函数由积分给出
函数由积分给出
 |
(8)
|
和级数
(Banderier 等人 2000)。
对于  ,
,
其中  是伽玛函数。类似地,
是伽玛函数。类似地,
 的渐近级数在复平面的不同象限中具有不同的形式,这种现象被称为斯托克斯现象。
的渐近级数在复平面的不同象限中具有不同的形式,这种现象被称为斯托克斯现象。
与艾里函数相关的函数被定义为
其中  是一个广义超几何函数。
是一个广义超几何函数。
Watson (1966, pp. 188-190) 给出了艾里函数一个稍微更通用的定义,作为艾里微分方程的解
 |
(21)
|
在原点处有限,其中  表示导数
表示导数  ,
,  , 并且允许任一符号。将这些解称为
, 并且允许任一符号。将这些解称为  , 则
, 则
 |
(22)
|
其中  是一个第一类贝塞尔函数。使用恒等式
是一个第一类贝塞尔函数。使用恒等式
 |
(25)
|
其中  是一个第二类修正贝塞尔函数,第二种情况可以重新表示为
是一个第二类修正贝塞尔函数,第二种情况可以重新表示为
另请参阅
Airy-Fock 函数,
艾里函数零点,
艾里 Zeta 函数,
第一类贝塞尔函数,
Map-Airy 分布,
第一类修正贝塞尔函数,
第二类修正贝塞尔函数
相关的 Wolfram 网站
http://functions.wolfram.com/Bessel-TypeFunctions/AiryAi/,
http://functions.wolfram.com/Bessel-TypeFunctions/AiryAiPrime/,
http://functions.wolfram.com/Bessel-TypeFunctions/AiryBi/,
http://functions.wolfram.com/Bessel-TypeFunctions/AiryBiPrime/
使用 探索
参考文献
Abramowitz, M. 和 Stegun, I. A. (编.). "Airy Functions." §10.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 446-452, 1972.Banderier, C.; Flajolet, P.; Schaeffer, G.; 和 Soria, M. "Planar Maps and Airy Phenomena." In Automata, Languages and Programming. Proceedings of the 27th International Colloquium (ICALP 2000) held at the University of Geneva, Geneva, July 9-15, 2000 (编. U. Montanari, J. D. P. Rolim, 和 E. Welzl). Berlin: Springer, pp. 388-402, 2000.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; 和 Vetterling, W. T. "Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions." §6.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 234-245, 1992.Sloane, N. J. A. Sequences A096714 和 A096715 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. 和 Oldham, K. B. "The Airy Functions Ai( ) and Bi(
) and Bi( )." Ch. 56 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 555-562, 1987.Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.
)." Ch. 56 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 555-562, 1987.Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.在 中被引用
艾里函数
请引用为
Weisstein, Eric W. "Airy Functions." 来自 —— 资源。 https://mathworld.net.cn/AiryFunctions.html
主题分类
,
,
, 和
。 其中,
和
是最常见的,而
和
则较少见。艾里函数常出现在物理学中,尤其是在光学、量子力学、电磁学和辐射传输中。
和
是 整函数。
和
函数在上面沿实轴绘制。
和
函数被定义为以下方程的两个线性独立解


是一个合流超几何极限函数。这些函数在 Wolfram 语言中实现为AiryAi[z] 和AiryBi[z]。它们的导数实现为AiryAiPrime[z] 和AiryBiPrime[z]。
, 这些函数可以写成
是一个第一类修正贝塞尔函数,而
是一个第二类修正贝塞尔函数。
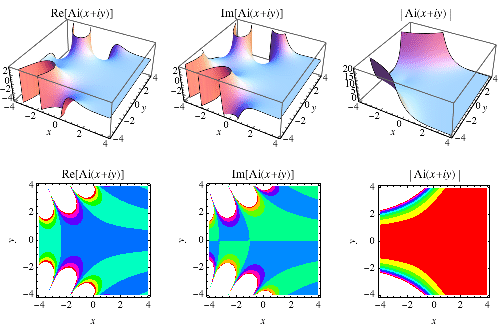
在复平面中的图示如上所示。
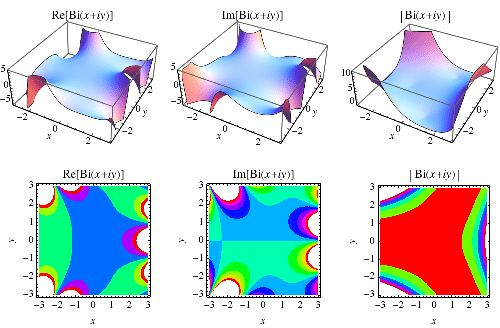
的图示也显示在上面。
函数由积分给出
![1/(3^(2/3)pi)sum_(n=0)^(infty)(Gamma(1/3(n+1)))/(n!)(3^(1/3)z)^nsin[(2(n+1)pi)/3]](/images/equations/AiryFunctions/Inline39.svg)
![1/(3^(1/6)pi)sum_(n=0)^(infty)(Gamma(1/3(n+1)))/(n!)(3^(1/3)z)^n|sin[(2(n+1)pi)/3]|](/images/equations/AiryFunctions/Inline42.svg)
,


是伽玛函数。类似地,

的渐近级数在复平面的不同象限中具有不同的形式,这种现象被称为斯托克斯现象。
是一个广义超几何函数。
表示导数
,
, 并且允许任一符号。将这些解称为
, 则
是一个第一类贝塞尔函数。使用恒等式
是一个第二类修正贝塞尔函数,第二种情况可以重新表示为
