紧致流形是作为拓扑空间是紧致的流形。例子包括圆(唯一的一维紧致流形)和维超球面和环面。二维紧致流形完全由它们的定向和洞的数量(亏格)分类。应该注意的是,术语“紧致流形”通常暗示“无边界流形”,这是此处使用的意义。当需要一个单独的术语时,紧致无边界流形被称为闭流形。
对于拓扑学和几何学中的许多问题,研究紧致流形很方便,因为它们具有“良好”的行为。使紧致流形“良好”的性质包括它们可以被有限多个坐标图覆盖,并且任何连续实值函数在紧致流形上都是有界的。
对于任何正整数,可以通过用莫比乌斯带替换
个圆盘来产生不同的不可定向曲面。 特别地,用莫比乌斯带替换一个圆盘会产生交叉曲面,而替换两个圆盘会产生克莱因瓶。球面,
洞环面,以及这一系列的不可定向曲面构成了紧致、无边界二维流形的完整列表。
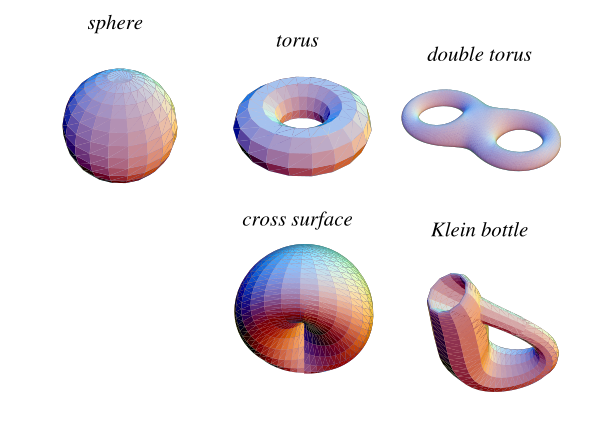
下表列出了小的二维紧致流形的类别,这些类别也在上面进行了说明。