五角二十四面体

制作你自己的五角二十四面体

打印并折叠

3D 打印

五角二十四面体是扭棱立方体的 24 面对偶多面体。上面展示了它的线框版本和一个可用于其构造的网格。

矿物赤铜矿 () 以五角二十四面体晶体的形式形成 (Steinhaus 1999, pp. 207 and 209)。

它是 Wenninger 对偶 (W₁₇)。

因为它是一个手性扭棱立方体的对偶，所以五角二十四面体也以两种对映异构形式出现，称为左旋（左）和右旋（右）。上面展示了两个对映体重叠在一起的吸引人的对偶。

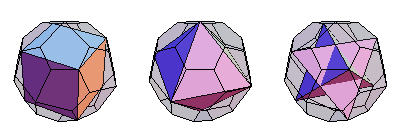
立方体、八面体和星形八面体都可以内接在五角二十四面体的顶点上 (E. Weisstein, Dec. 25, 2009)。

令人惊讶的是，三波那契常数 与五角二十四面体立方体的度量属性密切相关。

其不规则五边形面具有以下顶点角

			(1)
			(2)
			(3)

（四次）和

			(4)
			(5)
			(6)

（一次），其中 是一个多项式根， 是三波那契常数。

由单位边长的扭棱立方体形成的对偶具有以下边长

			(7)
			(8)
			(9)
			(10)
			(11)
			(12)

外接球半径 由下式给出

			(13)
			(14)
			(15)

表面积 由下式给出

			(16)
			(17)
			(18)

和体积 由下式给出

			(19)
			(20)
			(21)