主题
Search

120-胞

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook
120-cell

120-胞是一个有限的正则四维多胞形，其施莱夫利符号为 {5,3,3}。它也被称为超十二面体或百二十面体，由 120 个十二面体组成，每条边连接 3 个，以及 720 个五边形 (Coxeter 1973, p. 264)。120-胞有 600 个顶点 (Coxeter 1969) 和 1200 条边。它是六个正则多胞体之一。

在第 176 页之后的图中，Coxeter (1973) 对该多胞形进行了图示。

120-胞的对偶是 600-胞。

半径为 2sqrt(2)，边长为 3-sqrt(5) 的 120-胞的顶点由以下集合给出，其中 phi 是黄金比例 (Coxeter 1969, p. 404)。

1. 由 2(+/-1,+/-1,0,0) 及其所有排列给出的 24 个向量的集合。

2. 由 (+/-sqrt(5),+/-1,+/-1,+/-1) 及其所有排列给出的 64 个向量的集合。

3. 由 (+/-phi^(-2),+/-phi,+/-phi,+/-phi) 及其所有排列给出的 64 个向量的集合。

4. 由 (+/-phi^2,+/-phi^(-1),+/-phi^(-1),+/-phi^(-1)) 及其所有排列给出的 64 个向量的集合。

5. 由 (+/-phi^2,+/-phi^(-2),+/-1,0) 及其所有偶排列给出的 96 个向量的集合。

6. 由 (+/-sqrt(5),+/-phi^(-1),+/-phi,0) 及其所有偶排列给出的 96 个向量的集合。

7. 由 (+/-2,+/-1,+/-phi,+/-phi^(-1)) 及其所有偶排列给出的 192 个向量的集合。

在 4 维空间中，120-胞的顶点之间有 30 个不同的非零距离。

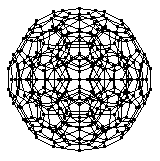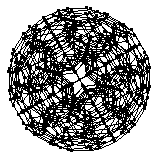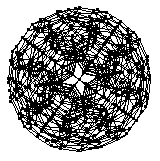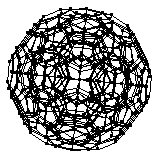
120-cell laser crystal (Bathsheba Grossman)
120-cell metal sculpture (Bathsheba Grossman)

上面的顶部图像显示了激光蚀刻到玻璃中的 120-胞的投影，底部的两个图像显示了可视化为金属雕塑的投影。这两件作品均由数字雕塑家 Bathsheba Grossman (http://www.bathsheba.com/) 创作。

120CellGraphs

120-胞的骨架，如上图所示的几个投影，是一个 4-正则图（即，周长为 5（五边形环）且直径为 15 的四次图）。从 120-胞骨架上的给定顶点开始，图距离为 n=0, 1, 2, ... 的顶点数为 1, 4, 12, 24, 36, 52, 68, 76, 78, 72, 64, 56, 40, 12, 4 和 1 (OEIS A108997)。120-胞具有图谱

4^1(alpha,beta,gamma)^(25)(mu,eta,sigma)^(36)[1/2(3+/-sqrt(13))]^(16)[1/2(-1+/-sqrt(21))]^(16)(-1+/-sqrt(2))^(48)[1/2(5+/-sqrt(5))]^91^(40)0^(18)(-1)^8(-2)^8(-3phi+2)^4(3phi-1)^4(+/-sqrt(5))^(24)phi^(24)(1-phi)^(24)(phi-2)^(24)(-1-phi)^(30),

其中 alpha, beta, 和 gamma 是 x^3-x^2-7x+4 的实根，mu, eta, 和 sigma 是 x^3-x^2-7x+8 的根，且 phi=(1+sqrt(5))/2 是黄金比例。120-胞的骨架在 Wolfram 语言中实现为GraphData["HundredTwentyCellGraph"].

120-胞骨架的独立数是 220 (Debroni et al. 2010)，其色数是 3 (S. Wagon 和 R. Pratt，私人通信，2011 年 12 月 2 日)。R. Pratt 还发现了一种平衡的 3-着色，每种颜色有 200 个顶点。

120-胞有

2^75^27^3(2^(114)3^(78)5^(20)7^(33)+2^(47)3^(18)5^27^(12)53^52311^3+239^23931^2) approx 2.760×10^(119)

个不同的网 (Buekenhout 和 Parker 1998)。其自同构群的阶数为 |Aut(G)|=120^2=14400 (Buekenhout 和 Parker 1998)。

另请参阅

11-胞, 16-胞, 24-胞, 57-胞, 600-胞, 胞, 超立方体, 五胞体, 多胞体, 多胞形, 单纯形

使用 Wolfram|Alpha 探索

参考文献

Buekenhout, F. and Parker, M. "维度 <=4 的正则凸多胞形的网的数量." Disc. Math. 186, 69-94, 1998.Coxeter, H. S. M. 几何学导论，第二版 New York: Wiley, p. 404, 1969.Coxeter, H. S. M. "星状 {5,3,3}." §14.2 in 正则多胞形，第三版 New York: Dover, pp. 136-137, 157, 264-267, and 292, 1973.Debroni, S.; Delisle, E.; Myrvold, W.; Sethi, A.; Whitney, J.; Woodcock, J.; Fowler, P. W.; de La La Vaissière, B.; and Deza, M. "120-胞和其他正则多面体的最大独立集." To appear in Ars Mathematica Contemporanea. 2010. http://www.liga.ens.fr/~deza/withFowler/120-cell_2010.pdf.Grossman, B. "120-胞." http://www.bathsheba.com/math/120cell/.Grossman, B. "120-胞晶体." http://www.bathsheba.com/crystalsci/120cell/.Sloane, N. J. A. Sequence A108997 in "整数序列在线百科全书."Stillwell, J. "120-胞的故事." Not. Amer. Math. Soc. 48, 17-24, 2001.Swab, E. "120-胞折叠图." http://users.adelphia.net/~eswab/120cell.htm.Weimholt, A. "120-胞折叠图." http://www.weimholt.com/andrew/120.html.Wells, D. 企鹅趣味几何词典。 London: Penguin, p. 210, 1991.

请引用为

Weisstein, Eric W. “120-胞。” 来自 MathWorld——Wolfram Web 资源。 https://mathworld.net.cn/120-Cell.html

主题分类