心形曲线

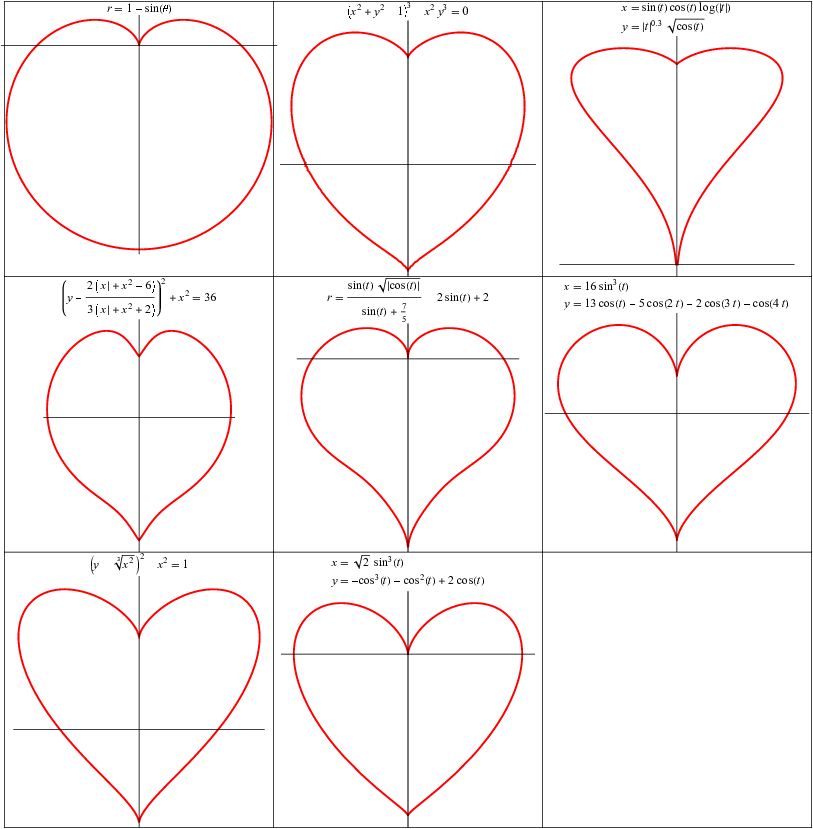
有许多数学曲线可以产生心形，上面展示了一些。 “第零”曲线是一个旋转的心脏线（其名称意为“心形”），由极坐标方程给出

第一个心形曲线是通过取横截面并将坐标重新标记为得到的，从而得到 6 阶代数方程

第二个心形曲线由参数方程给出

其中 (H. Dascanio, 私人通讯, 2003年6月21日)。

第三个心形曲线由下式给出

(P. Kuriscak, 私人通讯, 2006年2月12日)。这个心形曲线的每一半都是 6 阶代数曲线的一部分。

第四个曲线是极坐标曲线

来自匿名来源，并于 2010 年 2 月初从 Wolfram|Alpha 的日志文件中获得。这个心形曲线的每一半都是 12 阶代数曲线的一部分，因此整个曲线是 24 阶代数曲线的一部分。

第五个心形曲线可以参数化定义为

第六个心形曲线由简单的表达式给出

(由 J. Schroeder 在贺卡上注明，私人通讯，2021年10月16日)。当使用比例参数和正确无量纲化后，曲线变为

这可以写成关于和的六次方程。

第七个心形曲线可以参数化定义为

这是通过修改肾脏线的参数方程而产生的 (J. Mangaldan, 私人通讯, 2023年2月14日)。

这些心形的面积是

其中可以以闭合形式给出，作为超几何函数、反三角函数和伽玛函数的复杂组合。

Bonne 投影是一种地图投影，它将球体的表面映射到如上所示的心形区域。