主题
Search

狄利克雷 Beta 函数

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
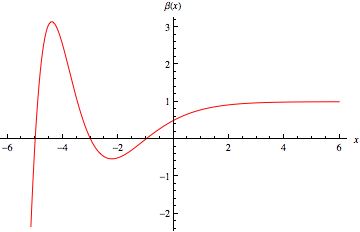
DirichletBetaReal
最小值 最大值
Powered by webMathematica
DirichletBetaReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

狄利克雷 beta 函数由以下求和定义

beta(x)=sum_(n=0)^(infty)(-1)^n(2n+1)^(-x)
(1)
=2^(-x)Phi(-1,x,1/2),
(2)

其中 Phi(z,s,a) 是 Lerch 超越函数。beta 函数可以用 Hurwitz zeta 函数 zeta(x,a) 表示为

beta(x)=1/(4^x)[zeta(x,1/4)-zeta(x,3/4)].
(3)

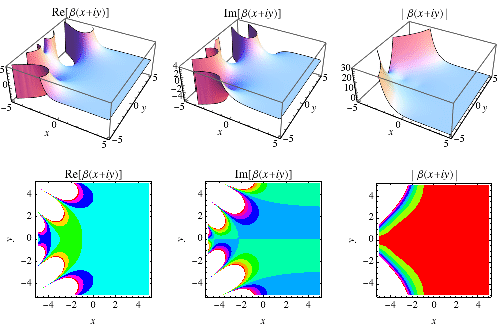
beta 函数可以使用解析延拓在整个复平面上定义，

beta(1-z)=(2/pi)^zsin(1/2piz)Gamma(z)beta(z),
(4)

其中 Gamma(z) 是 gamma 函数。

狄利克雷 beta 函数在 Wolfram 语言中实现为DirichletBeta[x].

beta 函数可以直接评估特殊形式的参数，如

beta(-2k)=1/2E_(2k)
(5)
beta(-2k-1)=0
(6)
beta(2k+1)=((-1)^kE_(2k))/(2(2k)!)(1/2pi)^(2k+1),
(7)

其中 E_n 是欧拉数。

的特定值包括

beta(1)=1/4pi
(8)
beta(2)=K
(9)
beta(3)=1/(32)pi^3
(10)
beta(4)=1/(768)[psi_3(1/4)-8pi^4],
(11)

其中 K 是 Catalan 常数，psi_n(x) 是多伽玛函数。对于 n=1, 3, 5, ..., beta(n)=rpi^n, 其中倍数是 1/4, 1/32, 5/1536, 61/184320, ... (OEIS A046976 和 A053005)。

它涉及以下积分

int_0^1int_0^1([-ln(xy)]^s)/(1+x^2y^2)dxdy=Gamma(s+2)beta(s+2)
(12)

(Guillera 和 Sondow 2005)。

Rivoal 和 Zudilin (2003) 证明了至少七个数字 beta(2), beta(4), beta(6), beta(8), beta(10), beta(12), 和 beta(14) 中有一个是无理数。

导数 beta^'(x)|_(x=n) 也可以在许多整数值 n 上进行解析计算，包括

beta^'(-1)=(2K)/pi
(13)
=0.583121808...
(14)
beta^'(0)=ln[(Gamma^2(1/4))/(2pisqrt(2))]
(15)
=0.391594392...
(16)
beta^'(1)=sum_(n=1)^(infty)((-1)^(n+1)ln(2n+1))/((2n+1))
(17)
=1/4pi{gamma+2ln2+3lnpi-4ln[Gamma(1/4)]}
(18)
=0.192901316...
(19)

(OEIS A133922, A113847, 和 A078127)，其中 K 是 Catalan 常数，Gamma(z) 是 gamma 函数，gamma 是 欧拉-马歇罗尼常数。

一个涉及 beta^'(n) 的漂亮求和由下式给出

sum_(k=1)^inftyln[((4k+1)^(1/(4k+1)^n))/((4k-1)^(1/(4k-1)^n))]=-beta^'(n)
(20)

对于正整数 n。

另请参阅

Catalan 常数, 狄利克雷 Eta 函数, 狄利克雷 Lambda 函数, Hurwitz Zeta 函数, Legendre's Chi 函数, Lerch 超越函数, 黎曼 Zeta 函数, Sierpiński 常数, Zeta 函数

使用 探索

参考资料

Abramowitz, M. 和 Stegun, I. A. (Eds.). 数学函数手册，包含公式、图表和数学表格，第 9 次印刷。 New York: Dover, pp. 807-808, 1972.Borwein, J. M. 和 Borwein, P. B. Pi & the AGM: 解析数论和计算复杂性研究。 New York: Wiley, p. 384, 1987.Comtet, L. 问题 37，高级组合数学：有限和无限展开的艺术，修订和扩充版。 Dordrecht, Netherlands: Reidel, p. 89, 1974.Guillera, J. 和 Sondow, J. "双重积分和无限乘积，用于通过 Lerch 超越函数的解析延拓获得一些经典常数。" 2005 年 6 月 16 日 http://arxiv.org/abs/math.NT/0506319.Rivoal, T. 和 Zudilin, W. "与 Catalan 常数相关的数字的丢番图性质。" Math. Ann. 326, 705-721, 2003. http://www.mi.uni-koeln.de/~wzudilin/beta.pdf.Sloane, N. J. A. 序列 A046976, A053005, A078127, A113847, 和 A133922 在 "整数序列在线百科全书" 中。Spanier, J. 和 Oldham, K. B. "Zeta 数和相关函数。" Ch. 3 在 函数图集。 Washington, DC: Hemisphere, pp. 25-33, 1987.Mathews, J. 和 Walker, R. L. 物理学的数学方法，第二版。 Reading, MA: W. A. Benjamin/Addison-Wesley, p. 57, 1970.

在 上引用

狄利克雷 Beta 函数

引用为

Weisstein, Eric W. “狄利克雷 Beta 函数。” 来自 —— 资源。 https://mathworld.net.cn/DirichletBetaFunction.html

主题分类