主题
Search

Adams' 圆

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
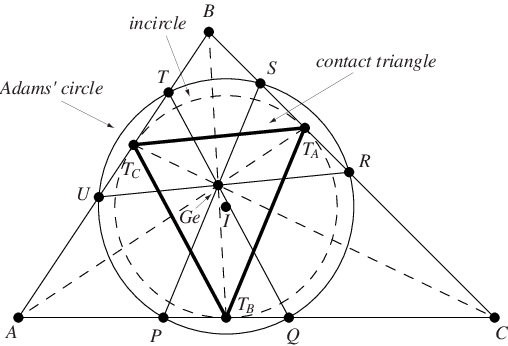
AdamsCircle

给定一个三角形 DeltaABC，构造切点三角形 DeltaT_AT_BT_C。现在从格尔贡点延伸平行于切点三角形各边的直线。这些直线相交于三角形 DeltaABC 的六个点 P、Q、R、S、T 和 U。C. 亚当斯在 1843 年证明了这些点共圆于一个现在被称为亚当斯圆的圆上。

亚当斯圆是一个中心圆，其圆函数为

l=(a(a-b-c)^3(ab+ac-2bc-b^2-c^2))/(bc(a^2+b^2+c^2-2ab-2bc-2ca)),
(1)

它不对应于任何著名的三角形中心。它的半径是复杂的表达式

R_A=(rsqrt(p^2-abcs-ps^2))/(p-s^2),
(2)

其中 r 是内切圆半径，s 是参考三角形的半周长，并且

p=ab+bc+ca.
(3)

亚当斯圆的圆心是 DeltaABC 的内心（Honsberger 1995，第 62-74 页）。

亚当斯圆上没有著名的三角形中心。

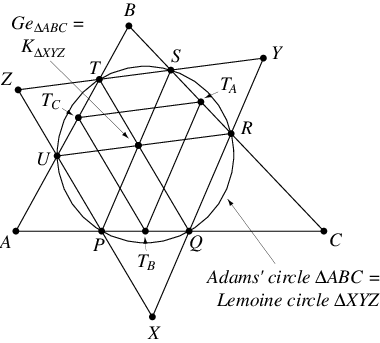
AdamsTriangle

延伸线段 UP、TS 和 RQ 以形成一个三角形 DeltaXYZ。那么 DeltaABC 的格尔贡点是 DeltaXYZ 的类似中线点，并且 DeltaABC 的亚当斯圆是 DeltaXYZ 的第一 Lemoine 圆（Honsberger 1995，第 98 页）。

另请参阅

切点三角形, 格尔贡点

使用 探索

参考文献

Adams, C. Die Lehre von den Transversalen. Witherthur, Germany: Steiner'schen Buchhandlung, 1843.Honsberger, R. "A Real Gem." §7.4 (v) in Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 62-64 and 98, 1995.Kimberling, C. "Triangle Centers and Central Triangles." Congr. Numer. 129, 1-295, 1998.Mackay, J. "Symmedians of a Triangle and their Concomitant Circles." Proc. Edinburgh Math. Soc. 14, 37-103, 1896.

在 中被引用

Adams' 圆

请引用为

Weisstein, Eric W. "Adams' 圆." 来自 网络资源。 https://mathworld.net.cn/AdamsCircle.html

主题分类