韦尔群

设 为有限维分裂 半单李代数，定义在特征为 0 的 域 上， 为分裂 卡 Cartan 子代数，且 为 在 的表示中的权。则

也是一个权。此外，反射 ，其中 是根，生成 中的线性变换群，称为 相对于 的韦尔群 ，其中 是 的 代数共轭空间，而 是由根张成的 Q-空间 (Jacobson 1979, pp. 112, 117, and 119)。

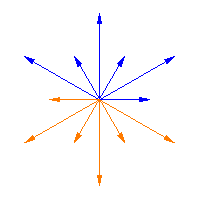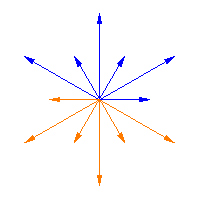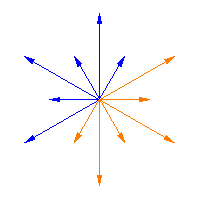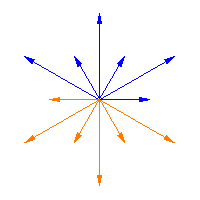
韦尔群作用于半单李代数的根，它是一个有限群。上面的动画展示了韦尔群作用于从一个韦尔矩阵到下一个韦尔矩阵的同伦的根上的这种作用（即，它将箭头从 滑动到 ），在前两个图中，而第三个图显示了韦尔群作用于半单李代数 的无限族的 Cartan 矩阵 的根（参见 Dynkin 图），这是 特殊线性李代数 。