速度向量

速度向量的概念来自经典物理学。通过使用向量表示单个粒子的位置和运动，运动方程变得更简单、更直观。假设粒子在时间 的位置由位置向量 给出。那么速度向量 是位置的导数，

例如，假设一个粒子被限制在平面上，其位置由 给出。那么它以恒定速度沿着单位圆运动。其速度向量是 。在图表中，将速度向量平移使其从 出发是有意义的。特别地，它被绘制为从 到 的箭头。

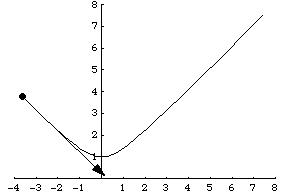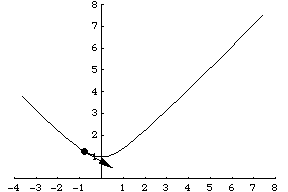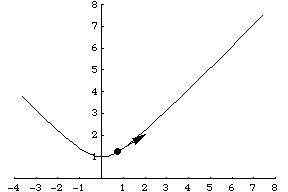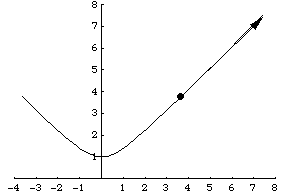
另一个例子是粒子沿着参数化表示为 的双曲线运动。其速度向量然后由 给出，如上图所示。

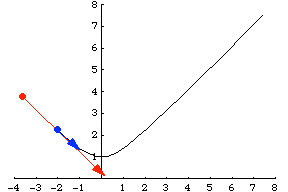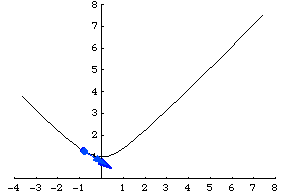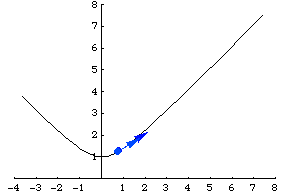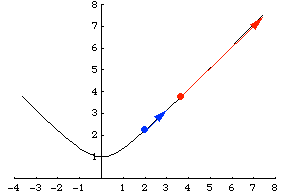
沿着相同的路径行进，但使用不同的函数称为重参数化，而链式法则描述了速度的变化。例如，双曲线也可以通过 参数化。请注意，，并且根据链式法则，。

请注意，可能的速度向量的集合形成一个向量空间。如果 和 是通过原点的两条路径，那么 也是，并且这条路径的速度向量是 。类似地，如果 是一个标量，那么路径 的速度向量是 。区分不同点的速度向量是有意义的。在物理学中，所有速度向量的集合给出了位置和动量的所有可能组合，被称为相空间。在数学中，速度向量形成切空间，而切空间的集合形成切丛。