
|
|
|
螺线截面是一环面与垂直于环面中平面且垂直于平面 的平面的交线的曲线方程。(环面与平面的通常交线称为环面截线)。设环面的管子半径为
,其中平面位于
平面内,并且管子的中心距离原点
。现在用平面
切割环面。具有
的环面方程给出以下方程
|
(1)
|
|
(2)
|
|
(3)
|
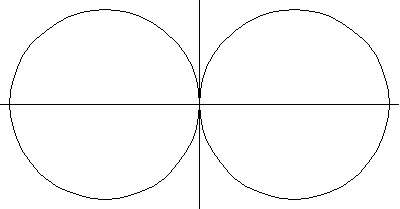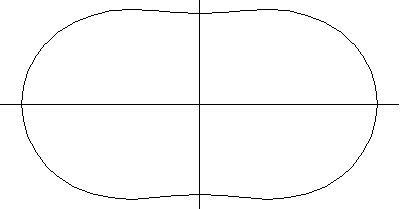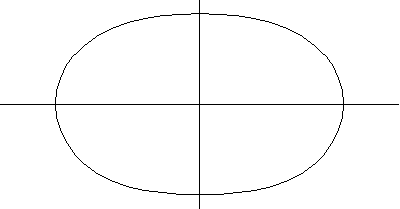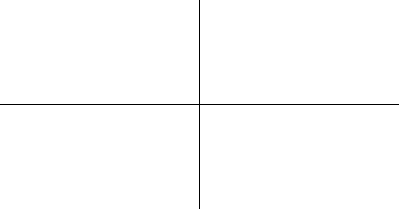
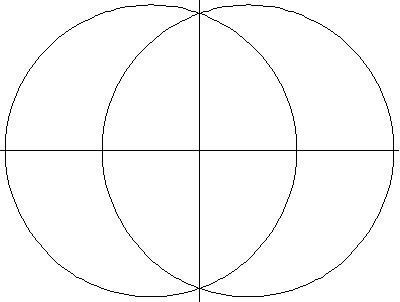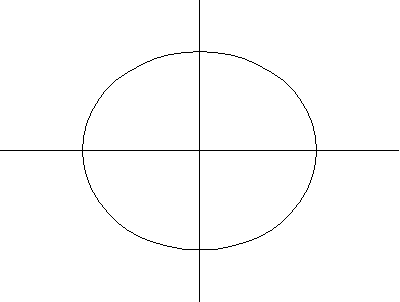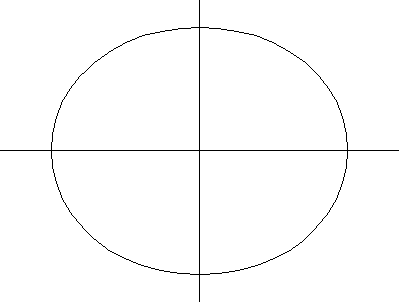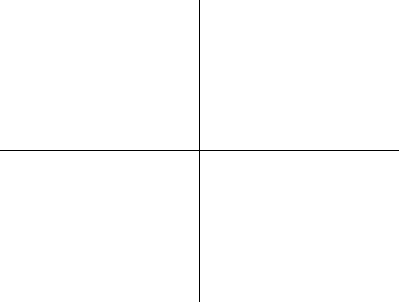
以上绘图分别显示了圆环环面、角环面和纺锤环面的一系列螺线截面。当 时,曲线由两个圆组成,半径为
,其中心位于
和
。如果
,则曲线由一个点(原点)组成;而如果
,则曲线上没有点。
螺线扩展是圆锥曲线的扩展,由梅内克缪斯(Menaechmus)在公元前 150 年左右通过用平面切割圆锥而构建,并由希腊数学家珀尔修斯(Perseus)在公元 50 年左右首次考虑(MacTutor)。
如果 ,则 (3) 简化为
|
(4)
|
这是卡西尼卵形线的方程。卡西尼卵形线因此是螺线截面。此外,以这些曲线作为横截面的表面是上面所示的卡西尼曲面,修改之处在于垂直分量是平方而不是四次方。