通过三角形质心 的给定三角形
和第二 Brocard 三角形的顶点对的三个外接圆被称为 McCay 圆(Johnson 1929, p. 306)。
它们的圆心(即第二 Brocard 三角形的圆心)的外接圆因此是Brocard 圆。
-McCay 圆的圆心函数为
和半径,
是 Neuberg 圆 的 1/3,其中 是 Brocard 角 (Johnson 1929, p. 307)。
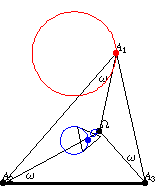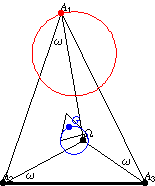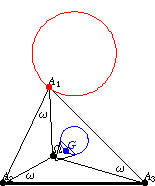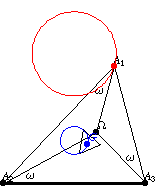
如果 多边形顶点 的 三角形 描述一个 Neuberg 圆
,那么它的三角形质心
描述其中一个 McCay 圆(Johnson 1929, p. 290)。在上图中,内三角形是
的第二 Brocard 三角形,其两个指示的边与
共圆在 McCay 圆上。