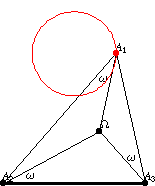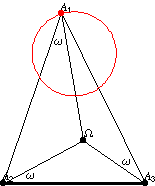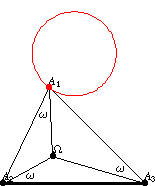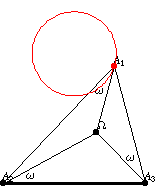
纽伯格 -圆是在给定底边
和给定布罗卡角
的三角形中,多边形顶点
的轨迹。从中心
,底边
对向角
。对于三角形的另外两条边,可以重复相同的步骤,总共得到三个纽伯格圆。类似地,通过主圆在三角形各自边上的反射,可以获得中心为
,
, 和
的三个反射纽伯格圆。
A-圆的方程可以通过将底边设为 (0, 0), (
, 0) 并解以下方程求得
|
(1)
| |||
|
(2)
|
同时使用以下公式消除 和
|
(3)
|
其中 是三角形
的面积。解 x 得
|
(4)
|
平方并完成平方后得到
|
(5)
|
因此,这条边上的纽伯格圆 的圆心为
|
(6)
|
半径为
|
(7)
|
纽伯格圆的圆心称为纽伯格中心,由纽伯格中心确定的三角形称为第一和第二纽伯格三角形。
没有任何 Kimberling 中心位于任何纽伯格圆或纽伯格反射圆上。
纽伯格圆的圆参数由下式给出
|
(8)
| |||
|
(9)
| |||
|
(10)
|
第一纽伯格三角形 (左图)和反射第一纽伯格三角形
(右图)如上图所示。
在给定直线的一侧作为底边,可以构造六个与给定不等边三角形直接或间接相似的三角形,并且这些三角形的顶点位于它们的公共纽伯格圆上(Johnson 1929,p. 289)。