蝴蝶定理

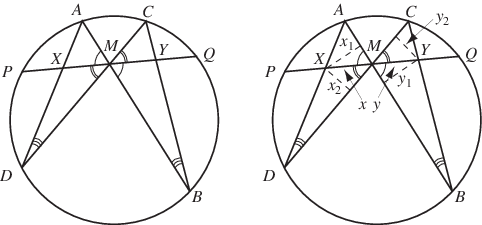
给定圆的一条弦，画出另外两条穿过其中点的弦和。将和的交点称为和。那么也是的中点。这个定理有很多证明方法，包括 W. G. Horner、Johnson (1929, p. 78) 和 Coxeter (1987, pp. 78 和 144) 的证明。后者简洁的证明采用了射影几何。

以下证明由 Coxeter 和 Greitzer (1967, p. 46) 给出。在右图中，从和向作垂线和，并从和向作垂线和。记，和，然后注意到根据相似三角形

(1)

(2)

(3)

因此

			(4)
			(5)

因此。证毕 (Q.E.D.)

另请参阅

更多尝试

Bogomolny, A. "蝴蝶定理。" http://www.cut-the-knot.org/pythagoras/Butterfly.shtml.Bogomolny, A. "一个更好的蝴蝶定理。" http://www.cut-the-knot.org/pythagoras/BetterButterfly.shtml.Bogomolny, A. "两个蝴蝶定理。" http://www.cut-the-knot.org/pythagoras/BetterButterfly.shtml.Coxeter, H. S. M. 射影几何，第二版 纽约: 施普林格出版社, pp. 78 和 144, 1987.Coxeter, H. S. M. 和 Greitzer, S. L. "蝴蝶定理。" §2.8 in 几何再探。 华盛顿特区: 美国数学协会, pp. 45-46, 1967.Johnson, R. A. 现代几何：三角形和圆的几何学基础论著。 波士顿, 马萨诸塞州: 霍顿·米夫林出版社, p. 78, 1929.