主题
Search

留数定理

一个 解析函数 f(z)，其 洛朗级数 由下式给出

f(z)=sum_(n=-infty)^inftya_n(z-z_0)^n,
(1)

可以使用围绕 围道 gamma 闭合的 z_0 逐项积分：

int_gammaf(z)dz=sum_(n=-infty)^(infty)a_nint_gamma(z-z_0)^ndz
(2)
=sum_(n=-infty)^(-2)a_nint_gamma(z-z_0)^ndz+a_(-1)int_gamma(dz)/(z-z_0)+sum_(n=0)^(infty)a_nint_gamma(z-z_0)^ndz.
(3)

柯西积分定理 要求第一项和最后一项消失，因此我们有

int_gammaf(z)dz=a_(-1)int_gamma(dz)/(z-z_0),
(4)

其中 a_(-1) 是复留数。使用 围道 z=gamma(t)=e^(it)+z_0 得到

int_gamma(dz)/(z-z_0)=int_0^(2pi)(ie^(it)dt)/(e^(it))=2pii,
(5)

因此我们有

int_gammaf(z)dz=2piia_(-1).
(6)

如果围道 gamma 包围多个极点，则该定理给出一般结果

int_gammaf(z)dz=2piisum_(a in A)Res_(z=a_i)f(z),
(7)

其中 A 是包含在围道内的极点集合。因此，这个惊人的定理表明，复平面中任何围道的围道积分的值仅取决于围道内几个非常特殊的点的性质。

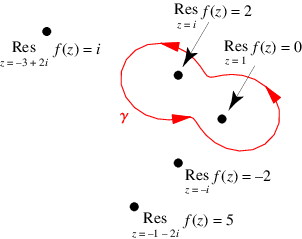
ResidueTheorem

上图显示了留数定理应用于所示围道 gamma 和函数的示例

f(z)=3/((z-1)^2)+2/(z-i)-2/(z+i)+i/(z+3-2i)+5/(z+1+2i).
(8)

只有极点 1 和 i 包含在围道内，它们的留数分别为 0 和 2。因此，围道积分的值由下式给出

int_gammaf(z)dz=2pii(0+2)=4pii.
(9)

另请参阅

柯西积分公式, 柯西积分定理, 复留数, 围道, 围道积分, 围道积分法, 群留数定理, 洛朗级数, 极点

使用 Wolfram|Alpha 探索

参考文献

Knopp, K. "The Residue Theorem." §33 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 129-134, 1996.Krantz, S. G. "The Residue Theorem." §4.4.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 48-49, 1999.

在 Wolfram|Alpha 中被引用

留数定理

请引用为

Weisstein, Eric W. "Residue Theorem." 来自 MathWorld--Wolfram 网络资源。 https://mathworld.net.cn/ResidueTheorem.html

主题分类