完美正方形剖分

一个正方形如果可以被剖分成若干个较小的正方形，且没有两个正方形相等，则称为完美正方形剖分（或平方正方形）。正方形剖分中，如果正方形不必大小不同，则称为珀金斯太太的被子。如果正方形的任何子集都不构成矩形，则称该完美正方形为“简单”的。

完美正方形剖分对应于平方数，这些平方数是平方数之和。因此，寻找这种正方形的最简单地方可能被认为是平方角锥数。然而，只有两个这样的数字：1 和 4900，即使

事实证明，不可能将这 24 个正方形排列成一个 正方形。

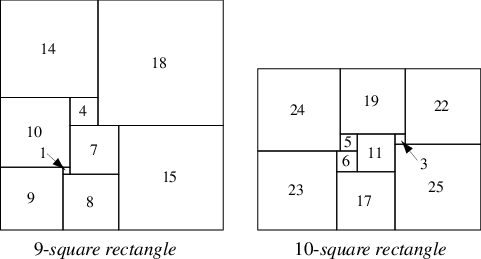
莫龙（1925）构造了一个 完美矩形，由九个不同大小的正方形组成（笛卡尔 1971），但卢津声称完美正方形不可能构造。当 R. 斯普拉格在 1939 年发表了一个 55 正方形的完美正方形时，这一论断被证明是错误的（威尔斯 1991）。莱歇特和特普金（1940）证明，一个矩形不能被剖分成少于九个不同的正方形（斯坦豪斯 1999，第 297 页）。

威尔科克斯随后发现了一个 24 正方形的完美正方形（威尔科克斯 1948, 1951；斯坦豪斯 1999，第 8-9 页）。

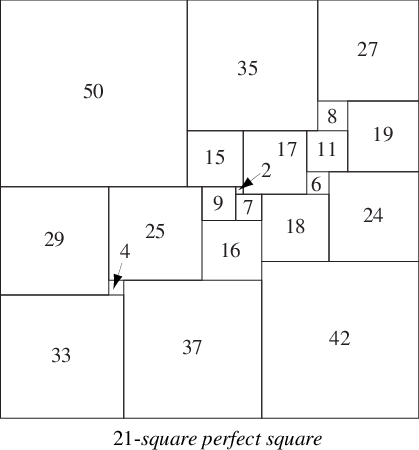
1978 年，A. J. W. 杜伊韦斯泰因（Bouwkamp 和 Duijvestijn 1992）发现了一个阶数为 21（可能的最低阶数）的唯一简单完美正方形。它由 21 个正方形组成，总边长为 112，如上图所示。

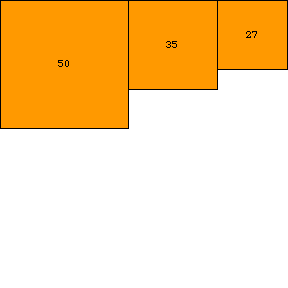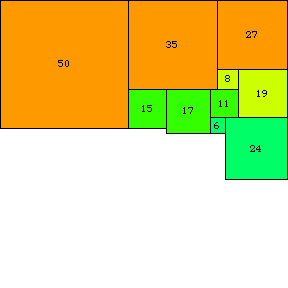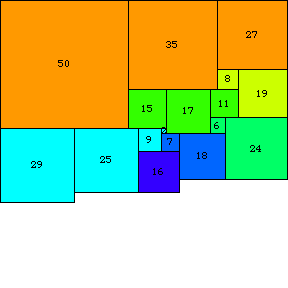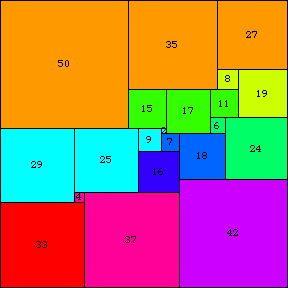
有一种简单的表示法（有时称为 Bouwkamp 代码）可以用来描述完美正方形。在这种表示法中，括号用于将顶部齐平的相邻正方形分组，然后将这些组按顺序放置在最高（和最左）可能的位置。例如，上面说明的 21 正方形表示为 [50, 35, 27], [8, 19], [15, 17, 11], [6, 24], [29, 25, 9, 2], [7, 18], [16], [42], [4, 37], [33]。

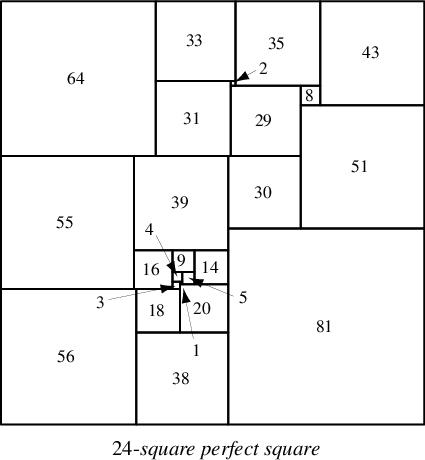
1940 年发现了一个边长为 608 的复合 26 完美正方形（Brooks 等人 1940；Kraitchik 1942，第 198 页）。贝勒 (1966) 说明了一个复合 28 正方形和一个简单 38 正方形。加德纳（1961，第 203 页和 206 页）说明了复合 39 正方形和 24 正方形。

阶数为 且 的简单完美正方形的数量为 1, 8, 12, 26, 160, 441, 1152, ... (OEIS A006983)。杜伊韦斯泰因的表 I 给出了 441 个 26 阶简单完美正方形的列表，其中最小的边长为 212，最大的边长为 825。斯金纳（1993）给出了简单完美平方正方形的最小可能边长（以及每个的最小阶数）为 110 (22)、112 (21)、120 (24)、139 (22)、140 (23)、...，复合完美平方正方形的最小可能边长（以及每个的最小阶数）为 175 (24)、235 (25)、288 (26)、324 (27)、325 (27)、...

实际上有三个边长为 110 的简单完美正方形。它们是 [60, 50], [23, 27], [24, 22, 14], [7, 16], [8, 6], [12, 15], [13], [2, 28], [26], [4, 21, 3], [18], [17]（22 阶；由 A. J. W. 杜伊韦斯泰因发现）；[60, 50], [27, 23], [24, 22, 14], [4, 19], [8, 6], [3, 12, 16], [9], [2, 28], [26], [21], [1, 18], [17]（22 阶；由 T. H. 威尔科克斯发现）；以及 [44, 29, 37], [21, 8], [13, 32], [28, 16], [15, 19], [12,4], [3, 1], [2, 14], [5], [10, 41], [38, 7], [31]（23 阶；由 A. J. W. 杜伊韦斯泰因发现）。

D. 斯莱托开发了一种高效的算法，用于查找非简单完美正方形，他称之为矩形和“L”形增长序列。该算法发现了一系列 24-32 阶的复合完美正方形。