紧致-开拓扑

紧致-开拓扑是函数空间上常用的一种拓扑。假设 和 是拓扑空间，C(X,Y) 是从 的连续映射的集合。C(X,Y) 上的紧致-开拓扑由以下形式的子集生成：

(1)

其中 是 中的紧致集， 是 中的开集。（因此得名“紧致-开”）。重要的是要注意，这些集合在交集下不是闭合的，并且不构成拓扑基。相反，集合 构成紧致-开拓扑的子基。也就是说，紧致-开拓扑中的开集是 的有限交集的任意并集。

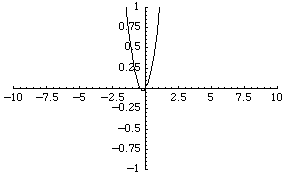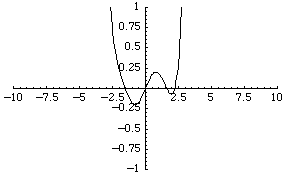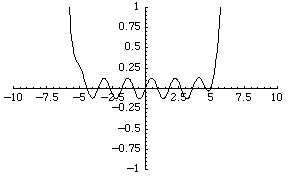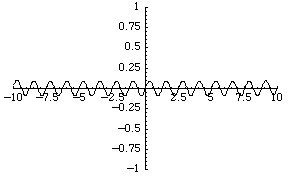
比较拓扑的最简单的函数空间是实值连续函数 的空间。函数序列 收敛到 当且仅当对于每个包含 的 ，除了有限个 外，包含所有 。因此，对于所有 和所有 ，存在一个 ，使得对于所有 ，

(2)

例如，函数序列 收敛到零函数，尽管每个函数都是无界的。

当 是度量空间时，紧致-开拓扑与紧致收敛的拓扑相同。如果 是局部紧 豪斯多夫空间，一个相当弱的条件，那么求值映射

(3)

由 定义的映射是连续的。类似地， 是连续的 当且仅当映射 ，由 给出，是连续的。因此，紧致-开拓扑是同伦理论中使用的正确拓扑。