边长为 的直角 等腰三角形膜的运动方程,其边沿正
轴和
轴方向,由下式给出
其中
且 ,
为 整数,其中
。此解可以通过从一个正方形膜的两个波动解中减去索引反转的解得到。由于对角线上与中心等距的点必须具有相同的波动方程解(通过对称性),因此只要
和
都是偶数或奇数,此过程给出的波函数将沿对角线消失。我们必须进一步限制模式,因为那些
的模式给出的波函数只是 负
,而
给出的波函数完全为零。
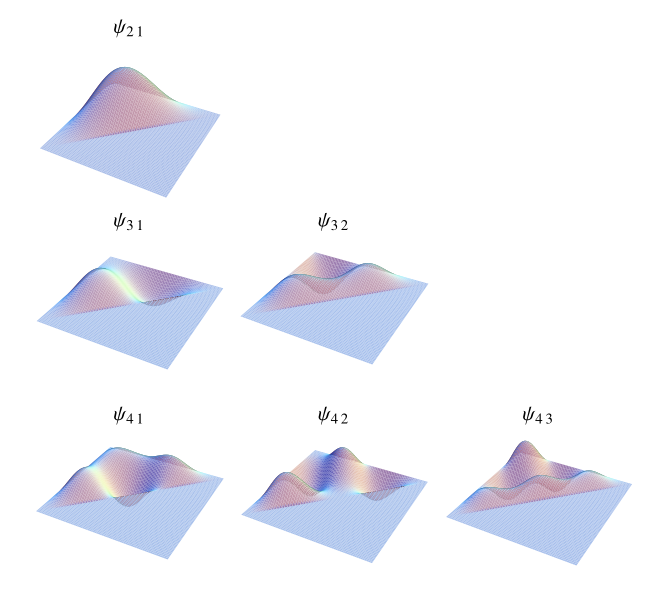
上面的图显示了最低阶的空间模式。

边长为 的直角 等腰三角形膜的运动方程,其边沿正
轴和
轴方向,由下式给出
其中
且 ,
为 整数,其中
。此解可以通过从一个正方形膜的两个波动解中减去索引反转的解得到。由于对角线上与中心等距的点必须具有相同的波动方程解(通过对称性),因此只要
和
都是偶数或奇数,此过程给出的波函数将沿对角线消失。我们必须进一步限制模式,因为那些
的模式给出的波函数只是 负
,而
给出的波函数完全为零。
上面的图显示了最低阶的空间模式。
Weisstein, Eric W. "波动方程——三角形。" 来自 —— 资源。 https://mathworld.net.cn/WaveEquationTriangle.html