一种在逻辑理论中使用的示意图,用于描绘集合的集合并表示它们之间的关系。
上面说明了关于两个和三个集合的韦恩图。二阶图(左图)由两个相交的圆组成,总共产生四个区域,、
、
和
(空集,由没有区域占据表示)。这里,
表示集合
和
的交集。
三阶图(右图)由三个对称放置的相互相交的圆组成,总共包含八个区域。标记为 、
和
的区域由仅在一个集合中且不在其他集合中的成员组成,标记为
、
和
的三个区域由在两个集合中但不在第三个集合中的成员组成,区域
由同时在所有三个集合中的成员组成,而没有区域占据则表示
。
一般来说, 阶韦恩图是平面上
条简单闭合曲线的集合,使得
1. 这些曲线将平面划分为 个连通区域,并且
2. 的每个子集
对应于一个由
中曲线的内部的交集形成的唯一区域 (Ruskey)。
由于有 (二项式系数)种方法从总共
个成员中选取
个成员,因此
阶韦恩图中的区域数量为
 |
(其中图表外部的区域包含在计数中)。
在每个圆的中心位于其他两个圆的交点的特殊情况下,三阶韦恩图中三个圆 的交集区域是被称为勒洛三角形的几何形状。
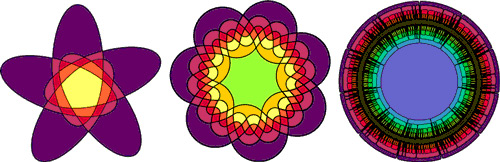
左上方左图显示了 Branko Grünbaum 的 韦恩图,而中间图中引人注目的 7 折叠玫瑰花形是 Ruskey 称为“维多利亚”的
韦恩图。右图显示了 Ruskey、Carla Savage 和 Stan Wagon 最近构建的
上的对称韦恩图。
在电视罪案剧《数字追凶》(NUMB3RS) 第 4 季剧集“权力”中,数学天才查尔斯·埃普斯构建了一个韦恩图,以确定符合特定描述且有暴力史的嫌疑人。