谱序列是同调代数中的一个工具,在代数、代数几何和代数拓扑中有着广泛的应用。 粗略地说,谱序列是一个用于跟踪具有相互映射的正合序列集合的系统。
谱序列有很多定义,并且存在许多细微的变体,这些变体在某些特定目的中非常有用。 最常见的类型是“第一象限上同调谱序列”,它是一系列阿贝尔群 ,其中
、
和
是整数,其中
和
为非负整数,且
对于某个正整数
,通常为 2。 群
配备有映射
|
(1)
|
使得
|
(2)
|
还有进一步的限制,即
|
(3)
|
映射 被称为边界映射。
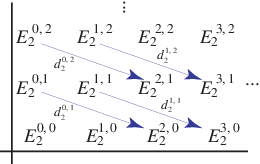
谱序列可以被可视化为一系列网格,每个网格对应一个 值。
和
表示网格上的位置,其中
是
坐标,
是
坐标。 上图显示了
的情况。
群 的整个集合及其边界映射被称为
-项。 群
完全由
-项确定
对于给定的 和
值,群
最终会稳定下来,因为只有有限数量的非零边界映射以该位置开始或结束。 这个稳定值被称为
。 稳定值允许定义谱序列的收敛性。 特别是,谱序列
收敛到群
,写作
|
(4)
|
如果存在一个滤子
|
(5)
|
使得连续商等于 项,即,
|
(6)
|
|
(7)
|
是一个纤维化(例如,Hopf 映射 )。 那么存在一个谱序列,其
-项为
|
(8)
|
该序列收敛到 。(这里,
表示普通上同调,与上面的
无关。) 这允许人们从其他两个空间的上同调计算三个空间
、
和
之一的上同调。
还有其他谱序列的例子。 Leray-Serre 谱序列用于计算层复形的超上同调。 Grothendieck 谱序列用于从两个原始函子的导出函子计算两个函子组合的导出函子。 Leray-Serre 谱序列是 Grothendieck 谱序列的一个特例。 最后,Adams 谱序列用于计算球体的高阶同伦群。