主题
Search

魔鬼曲线

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook
DevilsCurve

魔鬼曲线由 G. Cramer 于 1750 年和 Lacroix 于 1810 年研究 (MacTutor Archive)。它于 1858 年出现在 Nouvelles Annales 中。笛卡尔方程为

y^4-a^2y^2=x^4-b^2x^2,
(1)

等价于

y^2(y^2-a^2)=x^2(x^2-b^2),
(2)

极坐标方程为

r^2(sin^2theta-cos^2theta)=a^2sin^2theta-b^2cos^2theta,
(3)

参数方程为

x=costsqrt((a^2sin^2t-b^2cos^2t)/(sin^2t-cos^2t))
(4)
y=sintsqrt((a^2sin^2t-b^2cos^2t)/(sin^2t-cos^2t)).
(5)

上面所示的曲线对应于参数 a^2=1 和 b^2=2。

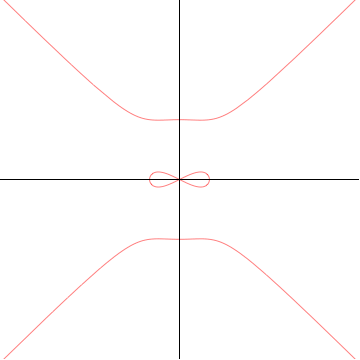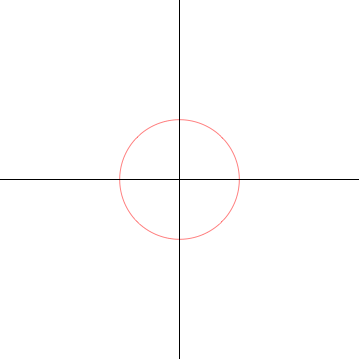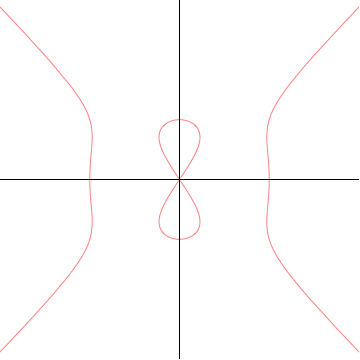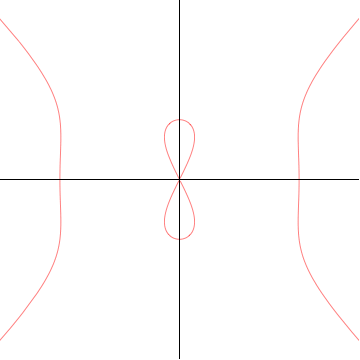
它在原点有一个叉点。

Devil's curve animation

对于 a/b<1，中心的沙漏是水平的，对于 a/b>1，它是垂直的，并且当它经过 a=b 时，曲线变为一个圆。

ElectricMotor

魔鬼曲线的一个特例是所谓的“电动马达曲线”

y^2(y^2-96)=x^2(x^2-100)
(6)

(Cundy 和 Rollett 1989)。

另请参阅

哑铃图, 蝴蝶曲线, 哑铃曲线, 八字曲线, 双纽线, 梨形曲线, 叉形分岔, 泪珠曲线

使用 Wolfram|Alpha 探索

参考文献

--. Nouvelle Annales, p. 317, 1858.Cramer, G. Introduction a l'analyse des lignes courbes algébriques. Geneva, p. 19, 1750.Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 71, 1989.Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 92-93, 1997.Lacroix, S. F. Traité du calcul différentiel et intégral, Vol. 1. Paris, p. 391, 1810.Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 151-152, 1972.MacTutor History of Mathematics Archive. "Devil's Curve." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Devils.html.Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. New York: Dover, p. 328, 1958.

请引用为

Weisstein, Eric W. "Devil's Curve." 来自 MathWorld——Wolfram 网络资源。 https://mathworld.net.cn/DevilsCurve.html

学科分类