C^infty 函数

一个 函数是指对于所有阶数求导都可微的函数。例如， (上图左侧) 是 函数，因为它的第 阶导数 存在且连续。所有多项式都是 函数。使用这种符号的原因是 C-k 函数具有 阶连续导数。

函数也称为“光滑”函数，因为它们及其导数都没有“角”，否则会使它们的图形看起来有些粗糙。例如， 不是光滑的（上图右侧）。

存在一些特殊的 函数，它们在分析和几何学中非常有用。例如，存在称为隆起函数的光滑函数，它们是特征函数的光滑近似。通常，这些函数需要一些微积分来证明它们确实是 函数。

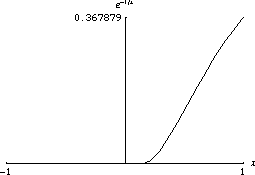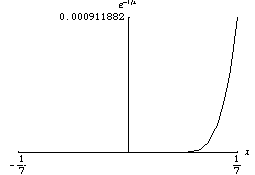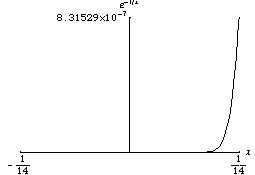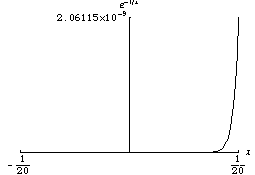
任何解析函数都是光滑的。但是光滑函数不一定是解析函数。例如，解析函数不能是隆起函数。考虑以下函数，它在 0 处的泰勒级数恒等于零，但该函数不为零

(1)

函数 非常迅速地趋于零。光滑函数的一个性质是它们在不同尺度下可能看起来非常不同。

光滑函数的集合不能构成巴拿赫空间，这使得一些问题变得困难，但它具有较弱的弗雷歇空间结构。