给定任意 开集 在
中,具有 紧闭包
, 存在 光滑函数 在
上恒等于 1,并且在
附近任意接近地消失。更精确地表达这一点的一种方式是,对于任何 开集
包含
, 存在一个 光滑函数
使得
1. 对于所有
并且
2. 对于所有
。
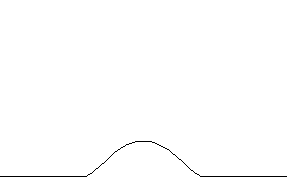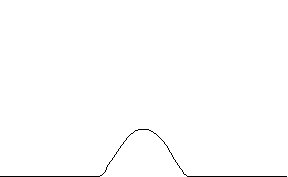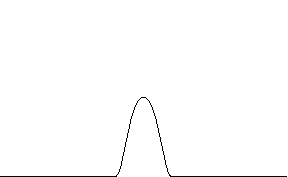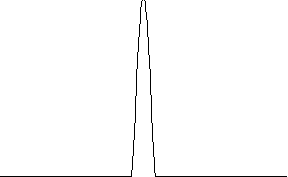
满足条件 (1) 和 (2) 的函数 被称为 bump 函数。如果
,那么通过重缩放
,即
,可以得到一个光滑函数序列,该序列收敛到 delta 函数,前提是
是 0 的邻域。
给定任意 开集 在
中,具有 紧闭包
, 存在 光滑函数 在
上恒等于 1,并且在
附近任意接近地消失。更精确地表达这一点的一种方式是,对于任何 开集
包含
, 存在一个 光滑函数
使得
1. 对于所有
并且
2. 对于所有
。

满足条件 (1) 和 (2) 的函数 被称为 bump 函数。如果
,那么通过重缩放
,即
,可以得到一个光滑函数序列,该序列收敛到 delta 函数,前提是
是 0 的邻域。
此条目由 托德·罗兰 贡献
罗兰,托德。“Bump 函数。” 来自 Web 资源,由 Eric W. Weisstein 创建。 https://mathworld.net.cn/BumpFunction.html