半圆

圆的一半。半径为 的半圆的面积由下式给出

			(1)
			(2)
			(3)

的加权平均值为

			(4)
			(5)

半圆是半球对于任何通过 z 轴的平面的横截面。

弯曲边界的周长由下式给出

(6)

使用 ，这给出

(7)

这个性质有时，尤其是在较旧的文献中，被称为半圆周。

半圆薄片的周长然后是其半圆周和直径之和

					(8)
					(9)
					(10)

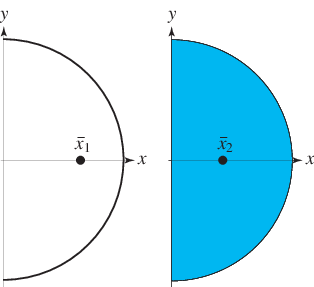
半圆曲线的 的加权值由下式给出

			(11)
			(12)
			(13)

因此几何质心为

(14)

半圆薄片的几何质心由下式给出

(15)

（Kern 和 Bland 1948，第 113 页）。