有三个与垂足圆相关的定理,统称为 Fontené 定理。
第一个 Fontené 定理是,设 为一个三角形,
为任意点,
为
的中点三角形,
为
关于
的垂足三角形。 将
和
的对应边的交点表示为
,
, 和
(例如,
是
和
的交点,等等),那么直线
,
和
交于一点
,该点
也位于
(即
的九点圆) 和
(即
关于
的垂足圆) 的外接圆上。
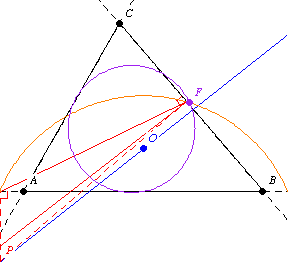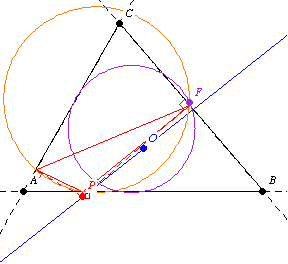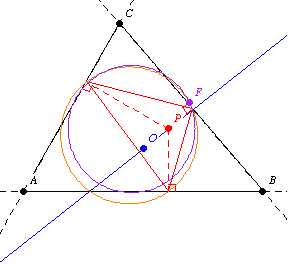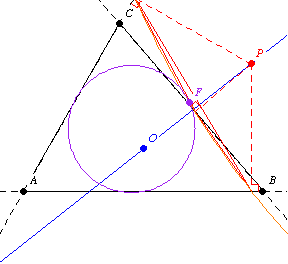
第二个 Fontené 定理指出,如果一个点在一个通过外心的固定线上移动,那么它的垂足圆会通过九点圆上的一个固定点,如上图所示。
第三个 Fontené 定理指出,点 的垂足圆与九点圆相切,当且仅当
及其等角共轭点
位于通过外心的直线上。(请注意,Johnson (1929) 错误地陈述了这个定理,用垂心代替了外心。)Feuerbach 定理是这个定理的一个特例。