主题
Search

标准映射

下载 Mathematica 笔记本下载 Wolfram 笔记本
StandardMap050
StandardMap100
StandardMap150
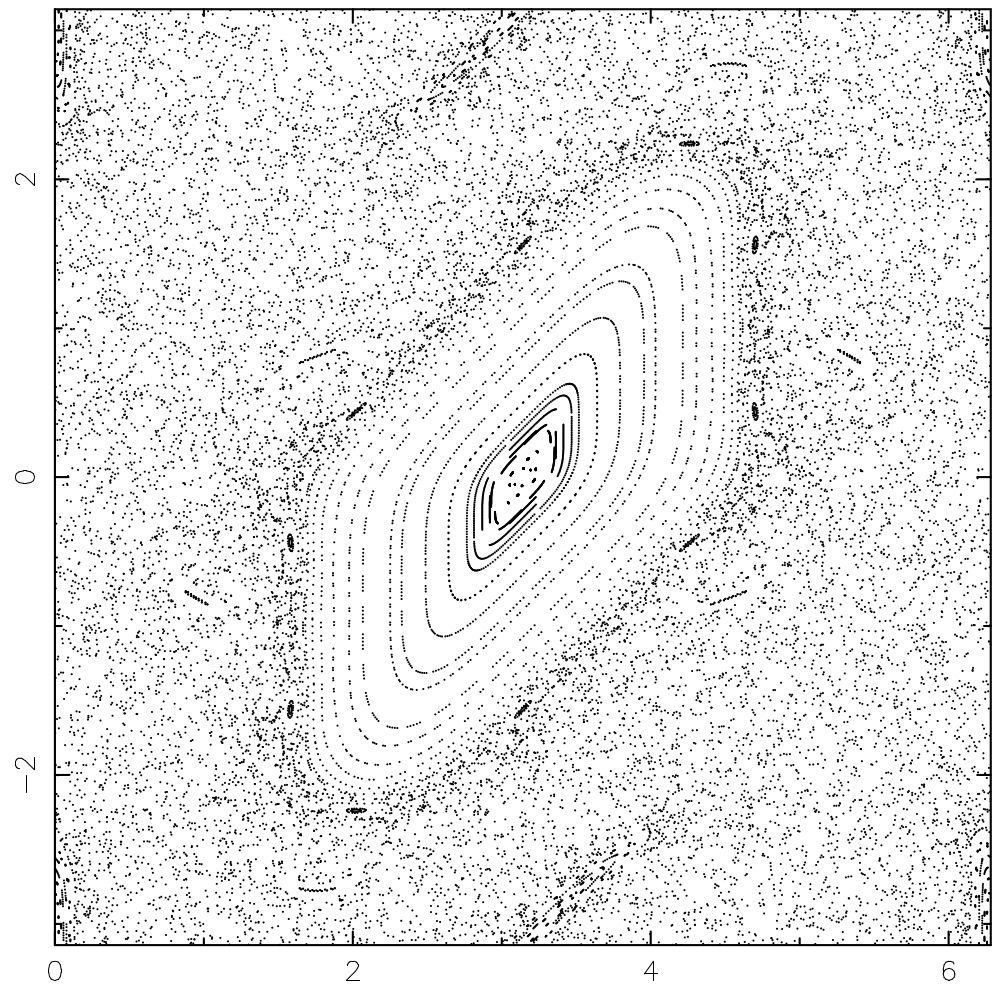
StandardMap200

一个二维映射，在一些较早的文献中也称为 Taylor-Greene-Chirikov 映射，定义为

I_(n+1)=I_n+Ksintheta_n
(1)
theta_(n+1)=theta_n+I_(n+1)
(2)
=I_n+theta_n+Ksintheta_n,
(3)

其中 I 和 theta 是以 2pi 为模计算的，K 是一个正常数。上面展示了常数 K 不同值的截面。

混沌区域宽度的解析估计 (Chirikov 1979) 发现

deltaI=Be^(-AK^(-1/2)).
(4)

数值实验给出 A approx 5.26 和 B approx 240。全局混沌发生的 K 值已被多位作者限定。格林方法是迄今为止设计的最精确的方法。

作者界限精确近似
Hermann>1/(34)0.029411764
Celletti 和 Chierchia (1995)>(419)/(500)0.838
Greene approx -0.971635406
MacKay 和 Percival (1985)<(63)/(64)0.984375000
Mather<4/31.333333333

不动点 通过要求以下条件找到

I_(n+1)=I_n
(5)
theta_(n+1)=theta_n.
(6)

第一个给出 Ksintheta_n=0，所以 sintheta_n=0 且

theta_n=0,pi.
(7)

第二个要求给出

I_n+Ksintheta_n=I_n=0.
(8)

因此，不动点是 (I,theta)=(0,0) 和 (0,pi)。为了进行线性稳定性分析，取变量的微分

dI_(n+1)=dI_n+Kcostheta_ndtheta_n
(9)
dtheta_(n+1)=dI_n+(1+Kcostheta_n)dtheta_n.
(10)

以矩阵形式，

[deltaI_(n+1); deltatheta_(n+1)]=[1 Kcostheta_n; 1 1+Kcostheta_n][deltaI_n; deltatheta_n].
(11)

特征值通过求解特征方程找到

|1-lambda Kcostheta_n; 1 1+Kcostheta_n-lambda|=0,
(12)

所以

lambda^2-lambda(Kcostheta_n+2)+1=0
(13)
lambda_+/-=1/2[Kcostheta_n+2+/-sqrt((Kcostheta_n+2)^2-4)].
(14)

对于不动点 (0,pi)，

lambda_+/-^((0,pi))=1/2[2-K+/-sqrt((2-K)^2-4)]
(15)
=1/2(2-K+/-sqrt(K^2-4K)).
(16)

如果 |R(lambda^((0,pi)))|<2.，不动点将是稳定的。这里，这意味着

1/2|2-K|<1
(17)
|2-K|<2
(18)
-2<2-K<2
(19)
-4<-K<0
(20)

所以 K in [0,4)。对于不动点 (0, 0)，特征值是

lambda_+/-^((0,0))=1/2[2+K+/-sqrt((K+2)^2-4)]
(21)
=1/2(2+K+/-sqrt(K^2+4K)).
(22)

如果对于较大的特征值映射是不稳定的，那么它就是不稳定的。因此，检查 lambda_+^((0,0))。我们有

1/2|2+K+sqrt(K^2+4K)|<1,
(23)

所以

-2<2+K+sqrt(K^2+4K)<2
(24)
-4-K<sqrt(K^2+4K)<-K.
(25)

但是 K>0，所以不等式的第二部分不可能为真。因此，映射在不动点 (0, 0) 处是不稳定的。

另请参阅

Hénon-Heiles 方程

使用 Wolfram|Alpha 探索

参考文献

Celletti, A. and Chierchia, L. "A Constructive Theory of Lagrangian Tori and Computer-Assisted Applications." Dynamics Rep. 4, 60-129, 1995.Chirikov, B. V. "A Universal Instability of Many-Dimensional Oscillator Systems." Phys. Rep. 52, 264-379, 1979.MacKay, R. S. and Percival, I. C. "Converse KAM: Theory and Practice." Comm. Math. Phys. 98, 469-512, 1985.Rasband, S. N. "The Standard Map." §8.5 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 11 and 178-179, 1990.Tabor, M. "The Hénon-Heiles Hamiltonian." §4.2.r in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 134-135, 1989.

在 Wolfram|Alpha 中被引用

标准映射

请按如下方式引用

Weisstein, Eric W. "标准映射。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/StandardMap.html

学科分类