主题
Search

追逐曲线

下载 Mathematica Notebook下载 Wolfram 笔记本

如果 A 沿着已知曲线移动，那么如果 P 始终朝向 A 且 A 和 P 以匀速运动，则 P 描述了一条追逐曲线。法国科学家皮埃尔·布格在 1732 年首次普遍考虑了追逐曲线，随后英国数学家布尔也进行了研究。

在电视剧NUMB3RS 第二季剧集 "Dark Matter" 中，数学天才查理·埃普斯在考虑神秘的第三名枪手的行动时，以 “路径最小化” 的名义提到了追逐曲线。

追逐方程由下式给出

(A-P)/(|A-P|)·(P^.)/(|P^.|)=1,
(1)

它指定了点 P 处的 切向量 始终平行于连接 A 和 P 的直线，并结合

P^.·P^.=1,
(2)

它指定了点 P 以恒定速度移动（不失一般性，在上面取为单位速度）。因此，将 (2) 代入 (1) 得出

((A-P)·P^.)/(|A-P|)=1.
(3)
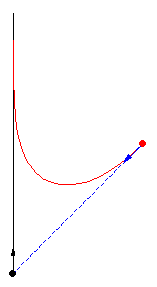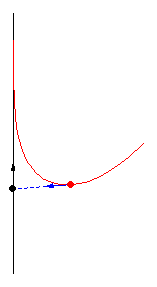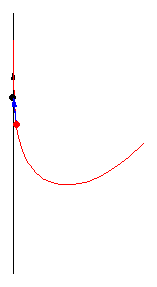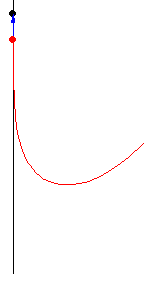
Pursuit curve for a straight vertical path

亚瑟·伯恩哈特（MacTutor Archive）研究了限制 A 为直线的案例。取 A(t)=(0,t) 的参数方程和点 P 的方程为 P=(x,y)，则此问题的运动方程由下式给出

1/(sqrt(x^2+(t-y)^2))[0-x; t-y]·[x^.; y^.]=1
(4)

和

x^.^2+y^.^2=1.
(5)

对 (4) 进行平方和重新排列得到

[(t-y)y^.-xx^.]^2=x^2+(t-y)^2.
(6)

展开得到

x^2(x^.^2-1)+2x(y-t)x^.y^.+(t-y)^2(y^.^2-1)=0,
(7)

可以使用 (5) 将其简化为

x^2y^.^2+2x(t-y)x^.y^.+(t-y)^2x^.^2=0.
(8)

但这是一个完全平方

[xy^.+(t-y)x^.]^2=0,
(9)

因此，对两边取平方根得到

xy^.+(t-y)x^.=0.
(10)

可以通过将两边除以 x^.，将此方程转换为 y 作为 x 函数的方程，得到

xy^'+t-y=0,
(11)

其中 y^'=y^./x^.=(dy/dt)/(dx/dt)=dy/dx。为了消除 t，请注意 P 行驶的弧长由下式给出

s=intsqrt(1+y^('2))dx=tv=t,
(12)

由于 v=1 对于此问题是常数，因此 (11) 变为

xy^'-y-intsqrt(1+y^('2))dx=0.
(13)

然后微分得到二阶常微分方程

xy^('')-sqrt(1+y^('2))=0
(14)

可以解析求解该方程以得到

y=c_1+c_2x^2-(lnx)/(8c_2).
(15)

正如预期的那样，解涉及两个任意常数 c_1 和 c_2，其值由初始条件固定。

粒子在时间 t=0 从 (x_0,y_0) 开始的初始条件由下式给出

y(x_0)=y_0
(16)
(dy)/(dx)|_(x_0)=(y_0)/(x_0).
(17)

将这些代入 (15)，求解 c_1 和 c_2，并将结果代回 (15) 得到完整解

y=1/4[(y_0+r_0)eta+(y_0-r_0)lneta+3y_0-r_0],
(18)

其中

eta=(x/(x_0))^2
(19)
r_0=sqrt(x_0^2+y_0^2).
(20)

P 的运动的 y 分量改变方向的点（对应于 y(x) 的最小值，其中 P 转向并开始从后面跟随追逐点）可以通过对 (18) 关于 x 求导，将其设置为 0，然后求解 x 来找到。结果是

x^*=x_0sqrt((r_0-y_0)/(r_0+y_0)).
(21)

代入并简化得到相应的 y 坐标，

y^*=(x_0y_0+2r_0y_0-r_0x_0)/(2(r_0+x_0))+1/4(y_0-r_0)ln((r_0-x_0)/(r_0+x_0)).
(22)

也可以用闭合形式表示 x(t) 和 y(t) 的解。将 (◇) 代入 (◇) 并求解 t 得到

t=xy^'-y=1/4[(eta-1)(r_0+y_0)+(r_0-y_0)lneta],
(23)

可以使用 兰伯特W函数 反转该式以获得

x(t)=x_0sqrt((W(chie^(chi-4t/(r_0-y_0))))/chi),
(24)

其中

chi=(r_0+y_0)/(r_0-y_0).
(25)

然后将其代入 y(x) 的方程得到

y(t)=1/4[3y_0-r_0+(y_0-r_0)ln((W(chie^(chi-4t/(r_0-y_0))))/chi)+(y_0+r_0)(W(chie^(chi-4t/(r_0-y_0))))/chi].
(26)
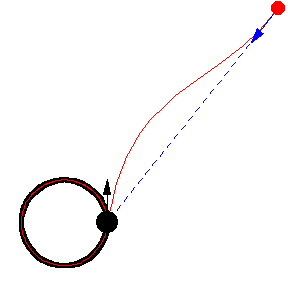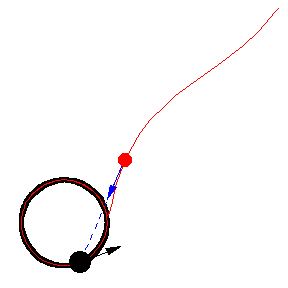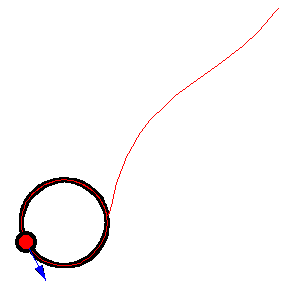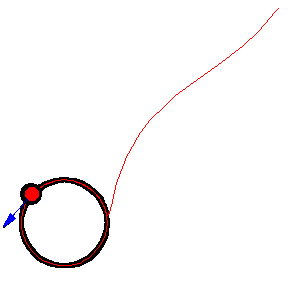
Outside the circle
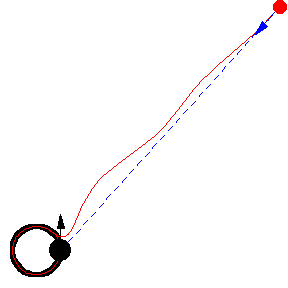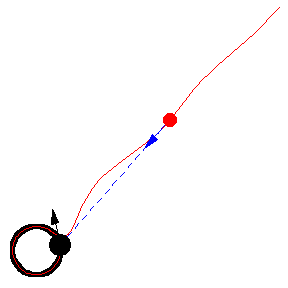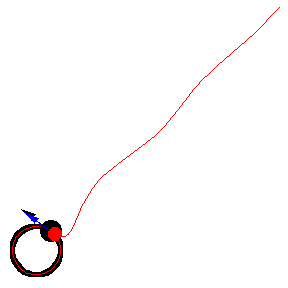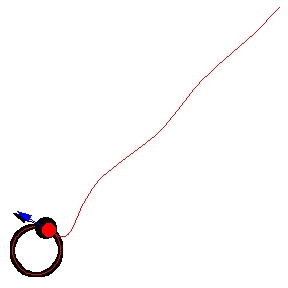
Further outside the circle
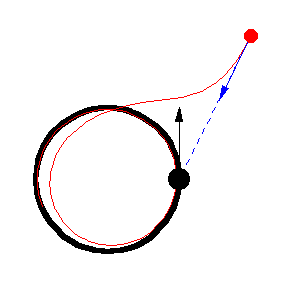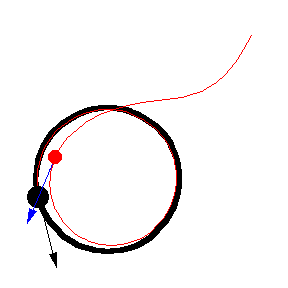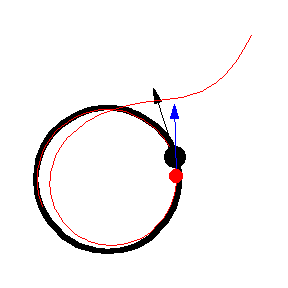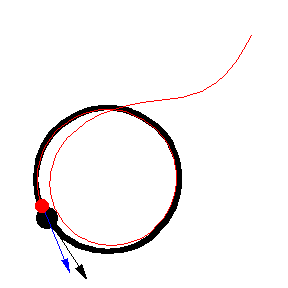
Outside the circle so curve cuts inside
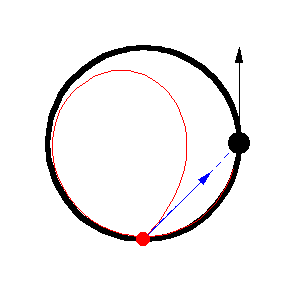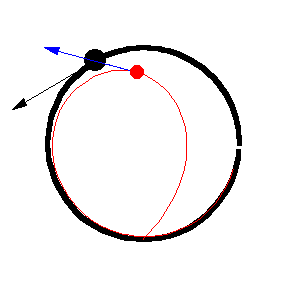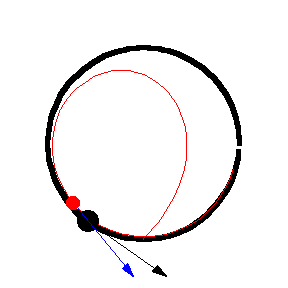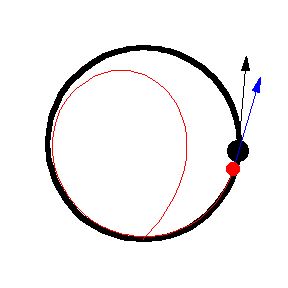
Inside the circle

上图显示了 A 以恒定速度绕圆移动的各种追逐曲线。

从正多边形的角开始并彼此奔跑的 n 只老鼠（或狗）的问题称为 老鼠问题。

另请参阅

阿波罗尼奥斯追逐问题, 布罗卡尔点, 老鼠问题, 曳物线, 拖网渔船问题, 漩涡线

使用 Wolfram|Alpha 探索

参考文献

Barton, J. C. and Eliezer, C. J. "On Pursuit Curves." J. Austral. Math. Soc. Ser. B 41, 358-371, 2000.Bernhart, A. "Curves of Pursuit." Scripta Math. 20, 125-141, 1954.Bernhart, A. "Curves of Pursuit-II." Scripta Math. 23, 49-65, 1957.Bernhart, A. "Polygons of Pursuit." Scripta Math. 24, 23-50, 1959.Bernhart, A. "Curves of General Pursuit." Scripta Math. 24, 189-206, 1959.MacTutor History of Mathematics Archive. "Pursuit Curve." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Pursuit.html.Simmons, G. F. Differential Equations, With Applications and Historical Notes. New York: McGraw-Hill, 1972.Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. New York: Dover, p. 327, 1958.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 201-202, 1991.Yates, R. C. "Pursuit Curve." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 170-171, 1952.

在 Wolfram|Alpha 中被引用

追逐曲线

引用为

Weisstein, Eric W. "追逐曲线。" 来自 MathWorld——Wolfram 网络资源。 https://mathworld.net.cn/PursuitCurve.html

主题分类