主题
Search

豆形曲线

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本

有几种被称为“豆形曲线”的平面曲线。

BeanCurve

Cundy 和 Rowllet (1989, p. 72) 提出的豆形曲线是由隐式方程给出的四次曲线

x^4+x^2y^2+y^4=ax(x^2+y^2).
(1)

它在 (2/3a,+/-2/3a) 处有水平切线，在 (0,0) 和 (a,0) 处有垂直切线。曲线围成的面积由下式给出

A=sqrt(2)a^2int_0^1sqrt(x(1-x+sqrt(1+(2-3x)x)))dx
(2)
=(7pia^2)/(12sqrt(3))
(3)
=1.058049...a^2
(4)

(OEIS A193505)。内部的几何质心 (x^_,y^_) 由下式给出

x^_=(23)/(42)a
(5)
y^_=0
(6)

内部的面积惯性矩张量由下式给出

I_(xx)=(113pi)/(1728sqrt(3))a^4
(7)
I_(xy)=0
(8)
I_(yy)=(23pi)/(108sqrt(3))a^4
(9)

(E. Weisstein，2 月 3-5 日，2018 年)。周长由下式给出

s=2aint_0^1sqrt(1+((1-2x+(1+3x-6x^2)/(sqrt(1+2x-3x^2)))^2)/(8x(1-x+sqrt(1+2x-3x^2))))dx
(10)
=3.75021364...a
(11)

(OEIS A193506)。

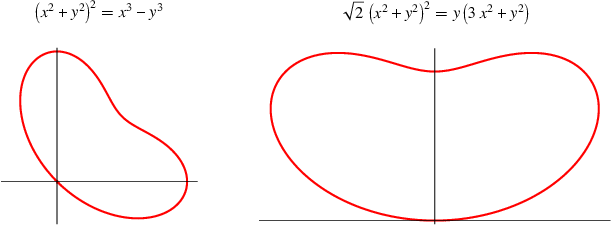
LimaBeanCurve

第二种豆形曲线更像实际的豆子（特别是利马豆），这里称为“利马豆曲线”，由简单的极坐标方程给出

r=a(sin^3theta+cos^3theta)
(12)

(Wassenaar；上图左侧)。它也是一条四次曲线，并具有笛卡尔方程

(x^2+y^2)^2=a(x^3+y^3).
(13)

如果利马豆旋转使其完全出现在 y>0 半平面中，并关于 x-轴对称定向（上图右侧），则其笛卡尔方程变为

sqrt(2)(x^2+y^2)^2=ay(3x^2+y^2).
(14)

原始极坐标曲线的参数方程为

x=acost(sin^3t+cos^3t)
(15)
y=asint(sin^3t+cos^3t).
(16)

这条曲线的最大值为 x_(max)=y_(max)=1，最小值为 x_(min)=y_(min)=r，其中 r=-0.28288... 是 27-27x-288x^2+512x^3=0 的实根。曲线围成的面积为

A=5/(16)pia^2
(17)
=0.98174770...a^2
(18)

(参见 OEIS A244978)。内部的几何质心 (x^_,y^_) 由下式给出

x^_=3/(10)a
(19)
y^_=3/(10)a,
(20)

周长由下式给出

s=aint_0^pisqrt(1+3/2sin^2(2theta)-2sin^3(2theta))dtheta
(21)
=1/2aint_0^(2pi)sqrt(1+3/2sin^2x-2sin^3x)dx
(22)
=aint_(-1)^1sqrt((2+3y^2-4y^3)/(2(1-y^2)))dy
(23)
=3.93170280...a
(24)

(OEIS A336501)。内部的面积惯性矩张量由下式给出

I=[(123pi)/(2048)a^4 -(9pi)/(1024)a^4; -(9pi)/(1024)a^4 (123pi)/(2048)a^4].
(25)

另请参阅

双尖瓣线, 蜗线

使用 Wolfram|Alpha 探索

参考文献

Cundy, H. and Rollett, A. 数学模型，第 3 版 Stradbroke, England: Tarquin Pub., p. 72, 1989.Sloane, N. J. A. 序列 A193505, A193506, A244978, 和 A336501，出自“整数数列线上大全”。Wassenaar, J. "数学曲线：豆形曲线 (1)。" http://www.2dcurves.com/quartic/quarticbn.htmlWassenaar, J. "数学曲线：豆形曲线 (2)。" http://www.2dcurves.com/quartic/quarticbn2.html

请引用本文为

韦斯坦因，埃里克·W. “豆形曲线”。来自 MathWorld——Wolfram Web 资源。 https://mathworld.net.cn/BeanCurve.html

主题分类